Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích hình chữ nhật ABCD là:
36 x 20 = 720 (cm2)
Vì AM= 1/3 MB => MB gấp 3 lần AM => AM = 36 : ( 3 + 1 ) = 9 (cm)
Mà chiều cao tam giác AMD chính là chiều rộng của hình chữ nhật ABCD
=> Diện tích tam giác AMD bằng:
( 9 x 20 ) : 2 = 90 (cm2)
Vì BN = NC => NC = 1/2 BC = 1/2 x 20 = 10 (cm)
Vậy diện tích tam giác NCD là:
( 10 x 63 ) : 2 = 180 (cm2)
Diện tích hình thang MBND là:
720 - 180 - 90 = 450 (cm2)

NGUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUU!

Diện tích hình chữ nhật ABCD là:
36 x 20 = 720 (cm2)
Vì AM= 1/3 MB => MB gấp 3 lần AM => AM = 36 : ( 3 + 1 ) = 9 (cm)
Mà chiều cao tam giác AMD chính là chiều rộng của hình chữ nhật ABCD
=> Diện tích tam giác AMD bằng:
( 9 x 20 ) : 2 = 90 (cm2)
Vì BN = NC => NC = 1/2 BC = 1/2 x 20 = 10 (cm)
Vậy diện tích tam giác NCD là:
( 10 x 63 ) : 2 = 180 (cm2)
Diện tích hình thang MBND là:
720 - 180 - 90 = 450 (cm2)

Diện tích ABM : 36 X 10 : 2 = 180 cm2
Diện tích ADN : 20 X 18 : 2= 180 cm2
Diện tích CMN : 10 X 18 : 2 = 90 cm2
Diện tích HCN ABCD : 20 X 36 = 720cm2
Diện tích cần tìm : 720 - 180 - 180 - 90 = 270 cm2
* Tỉ số % : 270 : 720 = 37,5%

Muốn tính diện tích hình tam giác MDN ta lấy diện tích hình vuông ABCD trừ đi tổng diện tích của ba hình tam giác vuông DAM, MBN và NCD
Ta có:
AM = MB = BN = NC = 20 : 2 = 10 (cm)
Diện tích hình tam giác DAM là:
20 x 10 : 2 = 100 ( cm2)
Diện tích hình tam giác MBN là:
10 x 10 : 2 = 50 (cm2)
Diện tích hình tam giác NCD là:
10 x 10 : 2 = 100 (cm2)
Diện tích hình vuông ABCD là:
20x 20 = 400 (cm2)
Vậy diện tích tam giác MDN là:
400 – (100 + 50 +1 00) = 150 (cm2)
bạn sai rùi, sao bên trên là 10 x 10 : 2 = 50, còn bên dưới thì lại 10 x 10 : 2 = 100
là sao

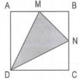
\(S_{MBND}=S_{ABCD}-S_{AMD}-S_{NCD}\)
\(S_{ABCD}=36\times20=720\left(cm^2\right)\)
\(AM=\frac{1}{3}MB\Rightarrow AM=\frac{1}{4}AB=\frac{1}{4}CD=9\left(cm\right)\)
\(BN=NC\Rightarrow NC=\frac{1}{2}BC=\frac{1}{2}AD=10\left(cm\right)\)
\(S_{AMD}=\frac{1}{2}AM\times AD=\frac{1}{2}\times20\times9=90\left(cm^2\right)\)
\(S_{NCD}=\frac{1}{2}NC\times CD=\frac{1}{2}\times10\times36=180\left(cm^2\right)\)
999999999999999999999999999999999