Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
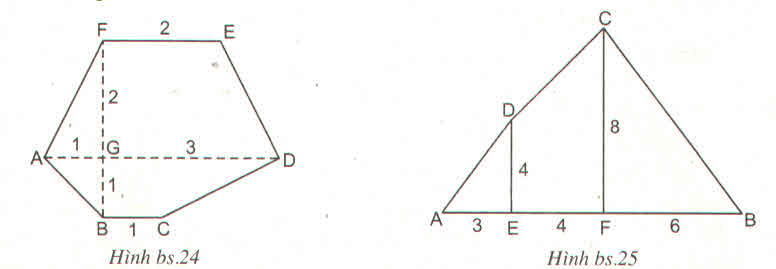
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)

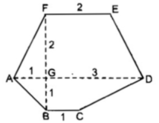
Ta chia đa giác ABCDEF thành hai hình thang ABCD và ADEF.
Hình thang ABCD có cạnh đáy BC = 1 (cm)
Đáy AD = AG + GD = 1 + 3 = 4 (cm)
Đường cao BG = 1 (cm)
S A B C D = (AD + BC) / 2.FG = (4 + 1) / 2 = 5/2 ( c m 2 )
Hình thang ADEF có đáy AD = 4 (cm)
S A D E F = (AD + EF) / 2.FG = (4 + 2) / 2. 2 = 6 ( c m 2 )
S A B C D E F = S A B C D + S A D E F = 5/2 + 6 = 17/2 ( c m 2 )
Đáy EF = 2cm, đường cao FG = 2cm
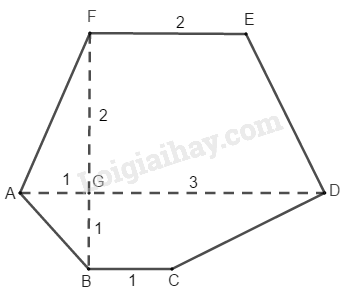

Diện tích đa giác ABCDEF là:
\(S_{ABCDEF}=S_{FGA}+S_{FEDG}+S_{BCDG}+S_{AGB}\\ =\dfrac{2.1}{2}+\dfrac{\left(2+3\right).2}{2}+\dfrac{\left(1+3\right).1}{2}+\dfrac{1.1}{2}\\ =1+5+2+0,5\\ =8,5\left(cm^2\right)\)
vì sao FEDG lại là hình thang ?