K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 9 2020
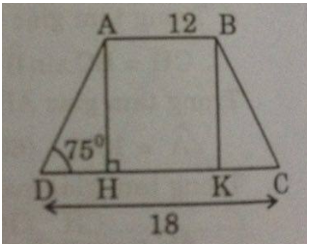
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, ˆD=75∘D^=75∘
Kẻ AH⊥CD,BK⊥CDAH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=167,94SABCD=AB+CD2.AH≈12+182.11,196=167,94 (cm2).
TT
2
24 tháng 7 2018
a) sin a=0,8
Ta có: \(\sin^2a+\cos^2a=1\)
\(\Rightarrow\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\orbr{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
24 tháng 7 2018
\(\sin a=0,8\)
\(\sin^2a=1-\sin^2a=1\)
\(\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\hept{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
Code : Breacker
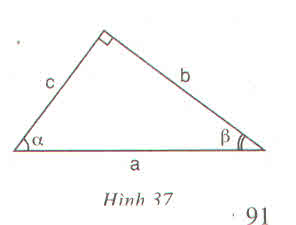
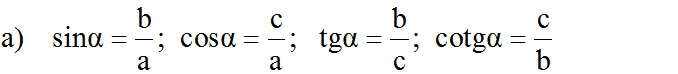
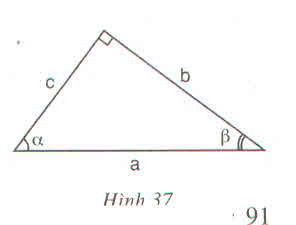
Vẽ \(\Delta\)ABC vuông tại A có B = 75°
=》 C = 90° - 75° = 15°
=》sinB = AC/BC
=> sin75° = AC/BC
=》 cos75° = AB/BC
=》 tan75° = AC/AB
=》 cot75° = AB/AC
@༒༎༊༗༛༚༘༔༐♡◇♧{Anh Tuấn}༲༮༯༳༵༱༰༴༶£¥♡♧♤□● : Tính ra giá trị luôn chứ ra tỉ số thì chỉ học cơ bản cũng tính được