K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TP
1
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Số tiền phải trả tương ứng với lượng điện 50kWh là:
\(50.1,678 = 83,9\) (nghìn đồng)
Số tiền phải trả tương ứng với lượng điện 100kWh là:
\(50.1,678 + (100 - 50).1,734 = 170,6\)(nghìn đồng)
Số tiền phải trả tương ứng với lượng điện 200kWh là:
\(50.1,678 + (100 - 50).1,734 + (200 - 100).2,014 = 372\)(nghìn đồng)
Điền vào bảng ta có:
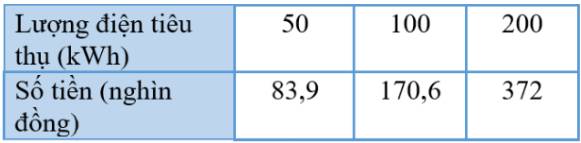
b) Công thức mô tả sự phụ thuộc y vào x khi\(0 \le x \le 50\) là:
\(y = 1,678.x\)
NC
1
LT
2
6 tháng 5 2016
Ta có:
\(A=3+\frac{3}{1+2}+\frac{3}{1+2+3}+...+\frac{3}{1+2+3+4+...+100}\)
\(A=3\left(1+\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+3+4+...+100}\right)\)
Đặt \(B=1+\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+3+4+...+100}\), khi đó ta đc:
\(B=1+\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+3+4+...+100}\)
Vì tổng số hạng bằng (số cuối + số đầu) . số số hạng : 2 nên ta có:
\(B=1+\frac{1}{\left(1+2\right).2:2}+\frac{1}{\left(1+3\right).3:2}+\frac{1}{\left(1+4\right).4:2}+...+\frac{1}{\left(1+100\right).100:2}\)
\(B=\frac{2}{1.2}+\frac{2}{2.3}+\frac{2}{3.4}+\frac{2}{4.5}+...+\frac{2}{100.101}\)
\(B=2\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{100.101}\right)\)
\(B=2\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{100}-\frac{1}{101}\right)\)
\(B=2.\left(1-\frac{1}{101}\right)\)
\(B=2.\frac{100}{101}=\frac{200}{101}\)
Ta có:
\(A=3.B\Rightarrow A=3.\frac{200}{101}=\frac{600}{101}\)
Vậy \(A=\frac{600}{101}\)
24 tháng 9 2016
Bài 1:
a)\(\begin{cases}\left(x-3\right)^2+\left(y+2\right)^2=0\\\begin{cases}\left(x-3\right)^2\ge0\\\left(y+2\right)^2\ge0\end{cases}\end{cases}\)
\(\Rightarrow\begin{cases}\left(x-3\right)^2=0\\\left(y+2\right)^2=0\end{cases}\)\(\Rightarrow\begin{cases}x=3\\y=-2\end{cases}\)
b) tương tự
24 tháng 9 2016
b) (x-12+y)200+(x-4-y)200= 0
\(\begin{cases}\left(x-12+y\right)^{200}+\left(x-4-y\right)^{200}=0\\\begin{cases}\left(x-12+y\right)^{200}\ge0\\\left(x-4-y\right)^{200}\ge0\end{cases}\end{cases}\)
\(\Rightarrow\begin{cases}\left(x-12+y\right)^{200}=0\\\left(x-4-y\right)^{200}=0\end{cases}\)\(\Rightarrow\begin{cases}x-12+y=0\\x-4-y=0\end{cases}\)\(\Rightarrow\begin{cases}x+y=12\left(1\right)\\x-y=4\left(2\right)\end{cases}\)
Trừ theo vế của (1) và (2) ta được:
\(2y=8\Rightarrow y=4\)\(\Rightarrow\begin{cases}x+4=12\\x-4=4\end{cases}\)\(\Rightarrow x=8\)
Vậy x=8; y=4
LA
2 tháng 2 2020
\(F=\)\(\frac{x^2+y^2}{x-y}=\frac{\left(x-y\right)^2+2xy}{x-y}=x-y+\frac{2xy}{x-y}\)
\(F\ge2\sqrt{2xy}=40\sqrt{5}\left(AM-GM\right)\)
Dấu "=" xảy ra : \(\left\{{}\begin{matrix}x-y=\frac{2xy}{x-y}\\xy=1000\\x>y\end{matrix}\right.\)
giải hệ
\(\Rightarrow\left\{{}\begin{matrix}x=10\sqrt{15}+10\sqrt{5}\\y=10\sqrt{15}-10\sqrt{5}\end{matrix}\right.\)
P = 4
NM
Cho A={1; 2; 3;...; 1000}. Hỏi có bao nhiêu số thuộc A chia hết cho ít nhất 1 trong 4 số 2, 3, 5, 7?
0
18 tháng 11 2022
a: BCNN(30;150)=150
b: BCNN(40;28;140)=280
c: BCNN(100;120;200)=600
A=100^2+(100x2)^2+....+(100x10)^2
A=100^2+100^2x2^2+.....+100^2x10^2
A=100^2(1+2^2+....+10^2)
A=100^2x385
A=3850000