Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(M\left(0;m\right)\in Oy\), đường thẳng d đi qua M, hệ số góc k có phương trình : \(y=kx+m\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=kx+m\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2x}{\left(x-1\right)^2}+m\Leftrightarrow\left(m-1\right)x^2-2\left(m+1\right)x+m+1=0\) (*)
Để từ M chỉ kẻ được đúng một tiếp tuyến đến đồ thị hàm số đã cho \(\Leftrightarrow\) (*) có đúng 1 nghiệm.
Do (*) không có nghiêm x = 1 nên (*) có đúng 1 nghiệm
\(\Leftrightarrow\left[\begin{array}{nghiempt}m=1\\\Delta'=2m+2=0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}m=1\\m=-1\end{array}\right.\)
Vậy có 2 điểm \(M_1\left(0;1\right);M_2\left(0;-1\right)\) thỏa mãn bài toán

Xét điểm \(M\left(m;0\right)\in Ox\).
Đường thẳng d đi qua M, hệ số góc k có phương trình : \(y=k\left(x-m\right)\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}-x^3+3x+2=k\left(x-m\right)\\-3x^2+3=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(3\left(x^2-1\right)\left(x-m\right)-\left(x^3-3x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2-3\left(1+m\right)x+3m\right)-\left(x+1\right)\left(x^2-x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[2x^2-\left(3m+2\right)x+3m+2\right]=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\\2x^2-\left(3x+2\right)x+3m+2=0\left(a\right)\end{array}\right.\)
Để từ M kẻ được 3 tiếp tuyến thì (a) phải có 2 nghiệm phân biệt khác -1
\(\begin{cases}\Delta=\left(3m+2\right)\left(3m-6\right)>0\\3m+3\ne0\end{cases}\)\(\Leftrightarrow\begin{cases}m< -\frac{2}{3}Vm>2\\m\ne-1\end{cases}\) (*)
Gọi \(x_1;x_2\) là 2 nghiệm của (a), khi đó hệ số góc của 3 tiếp tuyến là :
\(k_1=-3x_1^2+3;k_2=-3x_2^2+3;k_3=0\)
Để 2 trong 3 tiếp tuyến này vuông góc với nhau \(\Leftrightarrow k_1.k_2=-1\)
\(\Leftrightarrow9\left(x^2_1-1\right)\left(x^2_2-1\right)=1\Leftrightarrow9x^2_1x^2_2-9\left(x_1+x_2\right)^2+18x_1x_2+8=0\left(i\right)\)
Mặt khác, theo định lý Viet, \(x_1+x_2=\frac{3m+2}{2};x_1x_2=\frac{3m+2}{2};\)
Từ đó (i) \(\Leftrightarrow9\left(3m+2\right)+8=0\Leftrightarrow m=-\frac{26}{27}\) thỏa mãn điều kiện (*)
Vậy \(M\left(-\frac{26}{27};0\right)\) là điểm cần tìm

Giao điểm của đồ thị hàm số (C) và trục tung là điểm N(0;1)
Ta có : \(f'\left(x\right)=\frac{3}{\left(1-x\right)^2}\) suy ra tiếp tuyến tại điểm N là \(\left(\Delta\right):y=3x+1\Leftrightarrow\left(\Delta\right):3x-y+1=0\)
Xét điểm \(M\left(a+1;\frac{2a+3}{-a}\right)\in\left(C\right),a>0\)
Ta có : \(d_{M\\Delta }=\frac{\left|3\left(a+1\right)+\frac{2a+3}{a}+1\right|}{\sqrt{10}}=\frac{1}{\sqrt{10}}.\frac{3a^2+6a}{+3a}=\frac{3}{\sqrt{10}}\left(a+\frac{2}{a}+1\right)\ge\frac{3}{\sqrt{10}}\left(2\sqrt{2}+1\right)\)
Dấu bằng xảy ra khi \(a=\frac{2}{a}\Leftrightarrow a=\sqrt{2}\Rightarrow M\left(\sqrt{2}+1;\frac{2\sqrt{2}+5}{-\sqrt{2}}\right)\)

Phương trình tiếp tuyến \(\Delta\) tại \(M\left(x_0;-x^3_0+3x_0-2\right)\) là :
\(y=\left(-3x^2_0+3\right)\left(x-x_0\right)-x_0^3+3x_0-2\)
Gọi N (a;0) thuộc trục hoành. Vì \(N\in\Delta\) nên \(0=\left(-3x^2_0+3\right)\left(a-x_0\right)-x_0^3+3x_0-2\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x_0=1\\g\left(x_0\right)=2x_0^2+\left(2-3a\right)x_0+2-3a=0\end{array}\right.\) (*)
Để từ N kẻ được 3 tiếp tuyến đến (C) thì phương trình \(f\left(x_0\right)=0\) phải có hệ nghiệm phân biệt khác 1
Điều này tương đương với :
\(\begin{cases}\Delta=\left(2-3a\right)^2-8\left(2-3a\right)>0\\g\left(1\right)6-6a\ne0\end{cases}\) \(\Leftrightarrow a\in\left(-\infty;-2\right)\cup\left(\frac{2}{3};+\infty\right)\backslash\left\{1\right\}\)
Giả sử \(x_3=1\) thì \(x_1;x_2\) là nghiệm phương trình (*) nên theo Viet ta có :
\(\begin{cases}x_1+x_2=\frac{3a-2}{2}\\x_1.x_2=\frac{2-3a}{2}\end{cases}\)
Ta có \(x_1^3+x_2^3+x_3^3=21\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=20\)
\(\Leftrightarrow\left(3a-2\right)^3+6\left(3a-2\right)^2-160=0\)
\(\Leftrightarrow3a-2=4\Leftrightarrow a=2\) (thỏa mãn)
Vậy ta có \(N\left(2;0\right)\)

a) Ta có : \(y'=3x^2+2\left(m-1\right)x+m\left(m-3\right)\)
Hàm số (1) có cực đại và cực tiểu nằm 2 phía đối với trục tung <=> phương trình : \(3x^2+2\left(m-1\right)x+m\left(m-3\right)=0\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow P< 0\Leftrightarrow m\left(m-3\right)< 0\Leftrightarrow0< m< 3\)
Vậy \(0< m< 3\) là giá trị cần tìm
b) Khi m = 1 ta có : \(y=x^3-2x\).
Gọi \(M\left(a;a^3-2a\right)\in\left(C\right),a\ne0\)
Ta có \(y'=3x^2-2\) nên hệ số góc của \(\Delta\) là \(y'\left(a\right)=3a^2-2\)
Ta có \(\overrightarrow{OM}\left(a;a^3-2a\right)\) nên hệ số góc đường thẳng OM là \(k=a^2-2\)
Do đó : \(\Delta\perp OM\Leftrightarrow y'_a.k=-1\)
\(\Leftrightarrow\left(3a^2-2\right)\left(a^2-2\right)=-1\Leftrightarrow3a^4-8a^2+5=0\)
\(M_1\left(1;-1\right);M_1\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a^2=1\\a^2=\frac{5}{3}\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a=\pm1\\a=\pm\frac{\sqrt{5}}{3}\end{array}\right.\)(Thỏa mãn)
Suy ra có 4 điểm thỏa mãn đề bài :\(M_1\left(1;-1\right);M_2\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\)

Tập xác định : \(D=R\backslash\left\{1\right\}\)
\(M\in Ox\Rightarrow M\left(x_0;0\right)\) đường thẳng qua M với hệ số góc k có phương trình \(y=k\left(x-x_0\right)\) \(\left(\Delta\right)\)
\(\left(\Delta\right)\) là tiếp tuyến của đồ thì khi hệ \(\begin{cases}\frac{x^2}{x-1}=k\left(x-x_0\right)\\\frac{x^2-2x}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
\(\Rightarrow\frac{x^2}{x-1}=\frac{x^2-2x}{\left(x-1\right)^2}\left(x-x_0\right)\Leftrightarrow x\left[\left(x_0+1\right)x-2x_0\right]=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=0\\x=\frac{2x_0}{x_0+1}\end{array}\right.\) với \(x_0\ne-1\)
* Với \(x_0=0\Rightarrow k=0\)

Lấy \(M\left(m;m^4-5m^2+4\right)\in\left(C\right)\)
Suy ra phương trình (C) tại M : \(y=\left(4m^3-10m\right)\left(x-m\right)+m^4-5m^2+4\left(d\right)\)
Hoành độ của (d) và (C) là nghiệm của phương trình :
\(x^4-5x^2+4=\left(4m^3-10m\right)\left(x-m\right)+m^4-5m^2+4\)
\(\Leftrightarrow\left(x-m\right)^2\left(x^2+2mx+3m^2-5\right)=0\left(1\right)\)
Yêu cầu bài toán \(\Leftrightarrow x^2+2mx+3m^2-5=0\) có 2 nghiệm phân biệt khác m :
\(\Leftrightarrow\begin{cases}5-2m^2>0\\6m^2-5\ne0\end{cases}\)
Vậy \(m\in\left(-\frac{\sqrt{10}}{2};\frac{\sqrt{10}}{2}\right)\)\ \(\left\{\pm\frac{\sqrt{30}}{6}\right\}\)

Gọi k là hệ số góc của tiếp tuyến tại M, N thì \(x_M;x_N\) là nghiệm của phương trình :
\(f'\left(x\right)=k\Leftrightarrow3x^2-6x-k=0\)
Để tồn tại hai tiếp điểm M, N thì phải có \(\Delta'>0\Leftrightarrow k>-3\)
Ta có \(y=f'\left(x\right)\left(\frac{1}{3}x-\frac{1}{3}\right)-2x+2\)
Từ \(f'\left(x_M\right)=f'\left(x_N\right)=k\) suy ra phương trình đường thẳng MN là :
\(y=\left(\frac{k}{3}-2\right)x+2-\frac{k}{3}\), khi đó \(A\left(1;0\right);B\left(0;\frac{6-k}{3}\right)\)
Ta có \(AB^2=10\Leftrightarrow k=15\) (do k > -3)
Từ đó ta có 2 tiếp tuyến cần tìm là :
\(y=15x-12\sqrt{6}-15\)
\(y=15x+12\sqrt{6}-15\)

Chọn A.
Tiếp điểm nằm trên trục hoành nên ![]()
Ta có: 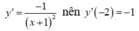
Vậy phương tình tiếp tuyến có dạng ![]()
![]()
Giao điểm của tiếp điểm vừa tìm với trục tung thỏa mãn hệ 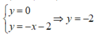
Xét \(M\left(0;m\right)\in Oy\). Đường thẳng d đi qua M, hệ số góc k có phương trình : \(y=kx+m\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}x^4-2x^2-1=kx+m\\4x^3-4x=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(-x^4-2x^2-1=4x^4-4x^2+m\)
\(\Leftrightarrow5x^4-2x^2+1+m=0\) (*)
Để từ M ta có thể kẻ đến đồ thị đúng 3 tiếp tuyến \(\Leftrightarrow\) (*) có 3 nghiệm phân biệt \(\Leftrightarrow m+1=0\Leftrightarrow m=-1\)
Khi đó (*) có 3 nghiệm \(x=0;x=\pm\sqrt{\frac{2}{5}}\) và 3 tiếp tuyến đó là :
\(y=-1;y=\pm\sqrt{\frac{2}{5}}x-1\)
Vậy \(M\left(0;-1\right)\) là điểm cần tìm