Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số xác định trên R khi và chỉ khi:
a.
\(\left(2m-4\right)x+m^2-9=0\) vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}2m-4=0\\m^2-9\ne0\end{matrix}\right.\) \(\Rightarrow m=2\)
b.
\(x^2-2\left(m-3\right)x+9=0\) vô nghiệm
\(\Leftrightarrow\Delta'=\left(m-3\right)^2-9< 0\)
\(\Leftrightarrow m^2-6m< 0\Rightarrow0< m< 6\)
c.
\(x^2+6x+2m-3>0\) với mọi x
\(\Leftrightarrow\Delta'=9-\left(2m-3\right)< 0\)
\(\Leftrightarrow m>6\)
e.
\(-x^2+6x+2m-3>0\) với mọi x
Mà \(a=-1< 0\Rightarrow\) không tồn tại m thỏa mãn
f.
\(x^2+2\left(m-1\right)x+2m-2>0\) với mọi x
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(2m-2\right)=m^2-4m+3< 0\)
\(\Leftrightarrow1< m< 3\)

ĐKXĐ: \(\left\{{}\begin{matrix}x-m+1\ge0\\-x+2m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge m-1\\x< 2m\end{matrix}\right.\)
\(\Rightarrow x\in[m-1;2m)\)
Để hàm xác định trên (3;4)
\(\Rightarrow\left(3;4\right)\subset[m-1;2m)\)
\(\Rightarrow\left\{{}\begin{matrix}m-1\le3\\2m\ge4\end{matrix}\right.\) \(\Rightarrow2\le m\le4\)

ĐKXĐ: \(\left(m+4\right)x^2-\left(m-4\right)x-2m+1\ge0\)
Xét \(m+4=0\Leftrightarrow m=-4\) => ..... (loại vì trường hợp này ràng buộc với x, ko thể với mọi x thuộc R được)
Xét \(m\ne-4\)
\(\Rightarrow\left\{{}\begin{matrix}m+4>0\\\Delta\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-4\\\left(m-4\right)^2-4\left(m+4\right)\left(1-2m\right)\le0\left(1\right)\end{matrix}\right.\)
(1) lúc này là phương trình b2, áp dụng dấu của tam thức bậc 2 để giải nhé :))
\(f\left(x\right)=\sqrt{\left(m+4\right)x^2-\left(m-4\right)x-2m+1}\) xđ với mọi x
\(\Leftrightarrow\left(m+4\right)x^2-\left(m-4\right)x-2m+1\ge0\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+4>0\\\left(m-4\right)^2-4.\left(m+4\right)\left(-2m+1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-4\\m^2-8m+16+8m^2+28m-16\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-4\\9m^2+20m\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-4\\-\frac{20}{9}\le x\le0\end{matrix}\right.\)
\(\Leftrightarrow-\frac{20}{9}\le x\le0\)

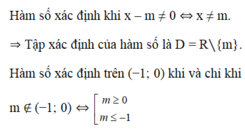
Để y xác định thì \(\left(m-2\right)x+2m-3\ge0\forall x\in\left[-1;4\right]\)
\(\Leftrightarrow mx-2x+2m-3\ge0\)
\(\Leftrightarrow m\left(x+2\right)-2x-3\ge0\)
\(\Leftrightarrow m\ge\dfrac{2x+3}{x+2}\left(x+2>0\forall x\in\left[-1;4\right]\right)\)
\(\Rightarrow1\le m\le\dfrac{11}{6}\)