Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=-3x^2+6x+m\)
Để hàm số nghịch biến trên \(\left(0;+\infty\right)\Rightarrow y'\le0\) \(\forall x>0\)
\(\Rightarrow-3x^2+6x+m\le0\Leftrightarrow3x^2-6x\ge m\)
Đặt \(f\left(x\right)=3x^2-6x\Rightarrow m\le\min\limits_{\left(0;+\infty\right)}f\left(x\right)=f\left(1\right)=-3\)
\(\Rightarrow m\le-3\)

Quân Trương: $m\leq 0$ hay $m\in (-\infty;0]$. Là đáp án A đấy bạn ơi

\(y'=-x^2+2mx+3m+2\)
Để hàm số nghịch biến trên R \(\Rightarrow y'\le0\) \(\forall x\in R\)
\(\Rightarrow\Delta'\le0\Leftrightarrow m^2+3m+2\le0\Rightarrow-2\le m\le-1\)

Chọn B.
Tập xác định ![]()
Có 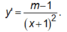
Hàm số nghịch bến trên mỗi khoảng của tập xác định
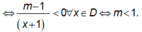

\(y'=-x^2+2mx+3m+2\)
Để hàm số nghịch biến trên R khi và chỉ khi:
\(\Delta'=m^2+3m+2\le0\Rightarrow-2\le m\le-1\)
\(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\) \(\Rightarrow a-3b=1\)
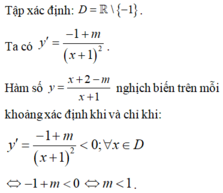

D=R
y' = -3x2 +6x+m <0
Để hàm nghịch biến trên khoảng (0; +∞) thì
Δ>0 và x1<x2≤0
\(\left\{{}\begin{matrix}m>-3\\x1+x2\\x1\cdot x2>0\end{matrix}\right.< 0\)