Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: m=-1/2
BPT sẽ là -2x-3/2-3>0
=>-2x>9/2
=>x<-9/4
=>Loại
TH2: m<>-1/2
Δ=(-2)^2-4(2m+1)(3m-3)
=4-4(6m^2-6m+3m-3)
=4-4(6m^2-3m-3)
=4-24m^2+12m+12
=-24m^2+12m+16
Để BPT vô nghiệm thì -24m^2+12m+16<=0 và 2m+1<0
=>m<-1/2 và \(\left[{}\begin{matrix}m< =\dfrac{3-\sqrt{105}}{2}\\m>=\dfrac{3+\sqrt{105}}{2}\end{matrix}\right.\)
=>\(m< =\dfrac{3-\sqrt{105}}{2}\)

Đáp án B
Đặt t = 2x > 1
PT
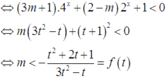
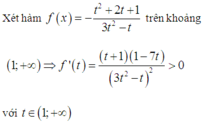
Dựa vào bảng biến thiên, suy ra m < -2

Đáp án C
Ta có : PT <=> log2 |cos x| – 2mlog|cos x| – m2 + 4 = 0
Đặt t = log|cos x|; t ∈ ( - ∞ ; 0 ]
Khi đó: t2 – 2mt – m2 + 4 = 0 (*)
PT đã cho vô nghiệm <= > (*) vô nghiệm hoặc có nghiệm dương.


Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
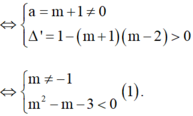
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
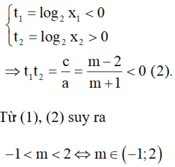
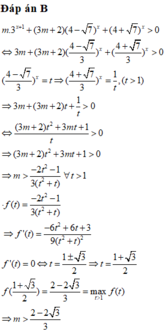
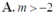
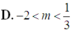

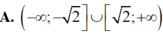




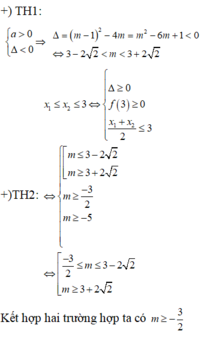
TH1: m=-1
BPT sẽ là:
-2(-1-1)x-3-3>0
=>4x-6>0
=>x>6/4
=>Loại
TH2: m<>-1
Δ=(2m-2)^2-4(m+1)(3m-3)
=4m^2-8m+4-4(3m^2-3)
=4m^2-8m+4-12m^2+12
=-8m^2-8m+16
Để BPT vô nghiệm thì -8m^2-8m+16<=0 và m+1<0
=>m^2+m-2>=0 và m<-1
=>(m+2)(m-1)>=0 và m<-1
=>(m>=1 hoặc m<=-2) và m<-1
=>m<=-2