ND
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 11 2017
1 a) \(\dfrac{\left(-2\right)}{5}\)= \(\dfrac{-6}{15}\); \(\dfrac{15}{-6}\)= \(\dfrac{5}{-2}\); \(\dfrac{-6}{-2}\)= \(\dfrac{15}{5}\); \(\dfrac{-2}{-6}\)= \(\dfrac{5}{15}\)
SG
5
18 tháng 4 2017
Đặt k = 
. Ta có x = 2k, y = 5k
Từ xy=10. suy ra 2k.5k = 10 => 10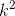 
= 10 => 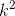= 1 => k = ± 1
Với k = 1 ta được = 1 suy ra x = 2, y = 5
Với k = -1 ta được = -1 suy ra x = -2, y = -5
TN
8 tháng 7 2017
Gọi \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
Với \(\dfrac{x}{2}=k\Rightarrow x=2k\); \(\dfrac{y}{5}=k\Rightarrow y=5k\)
Theo đề bài,ta còn có:
\(xy=10\)
hay 2k.5k=10
10k2 =10
\(\Rightarrow k=\pm1\)
Với k=1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=1\Rightarrow x=2;y=5\)
Với k=-1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=-1\Rightarrow x=-2;y=-5\)
16 tháng 9 2017
1/ a, Ta có :
\(x-2y+3z=35\)
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}=\dfrac{x-2y+3z}{3-8+15}=\dfrac{35}{10}=\dfrac{7}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{7}{2}\Leftrightarrow x=\dfrac{21}{2}\\\dfrac{x}{4}=\dfrac{7}{2}\Leftrightarrow y=14\\\dfrac{z}{5}=\dfrac{7}{2}\Leftrightarrow z=\dfrac{35}{2}\end{matrix}\right.\)
Vậy ..
CD
1
HH
16 tháng 12 2017
Ta có \(\frac{x+5}{2}=\frac{y-2}{3}\)và \(x-y=-10\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x+5}{2}=\frac{y-2}{3}=\frac{x+5-y-2}{2-3}=\frac{x-y+5-2}{2-3}=\frac{-10+5-2}{2-3}=\frac{-7}{-1}=7\)
=> \(\frac{x+5}{2}=7\)=> x + 5 = 14 => x = 9
và \(\frac{y-2}{3}=7\)=> y - 2 = 21 => y = 23
DH
15 tháng 7 2017
Bài 1:
\(A=\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}:\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{10}}\)
\(A=\dfrac{2.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}:\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{2}{7}.\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}\right)}\)
\(A=\dfrac{2}{7}:\dfrac{2}{7}=1\)
Bài 2: Here
Chúc bạn học tốt!!!
15 tháng 7 2017
1. Giải:
Gọi A =M : N
Ta có:M=\(\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}\)= \(\dfrac{2.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}\)=\(\dfrac{2}{7}\)
N=\(\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{10}}\)=\(\dfrac{2.\left(\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{10}\right)}{7.\left(\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{10}\right)}\)=\(\dfrac{2}{7}\)
Vậy A=M: N \(\Rightarrow\)A=\(\dfrac{2}{7}\):\(\dfrac{2}{7}\)=\(\dfrac{2}{7}\).\(\dfrac{7}{2}\)=\(\dfrac{2.7}{7.2}\)=1
2. Giải:
Với mọi x \(\in\)Q, ta luôn có \(x\) \(\le\) \(|x|\)(dấu bằng xảy ra khi x\(\ge\)0)
a)Nếu \(x+y\)\(\ge\)0 thì\(|x+y|=x+y\).
Vì \(x\le|x|,y\le|y|\)với mọi x, y\(\in\)Q nên:\(|x+y|=x+y\le|x|+|y|\)
b)Nếu x+y < 0 thì\(|x+y|=-\left(x+y\right)\)=\(-x-y\)
Mà -x\(\le\)\(|x|\), -y\(\le\)\(|y|\) nên: \(|x+y|\)= -x-y\(\le\)\(|x|+|y|\)
Vậy với mọi x, y\(\in\)Q ta đều có:\(|x+y|\le|x|+|y|\). Dấu bằng xảy ra khi x, y cùng dấu hoặc ít nhất có một số bằng 0.
14 tháng 5 2022
a: \(A=\dfrac{-1}{2}x^2y\cdot\dfrac{3}{2}xy=-\dfrac{3}{4}x^3y^2\)
\(B=x^2y^2\cdot y=x^2y^3\)
\(C=-\dfrac{1}{8}y^3x^2=-\dfrac{1}{8}x^2y^3\)
\(D=-x^2y^2\cdot\dfrac{-2}{3}x^3y=\dfrac{2}{3}x^5y^3\)
Các đa thức đồng dạng là B và C
b: \(\left\{{}\begin{matrix}-\dfrac{3}{4}x^3y^2>0\\-\dfrac{1}{8}x^2y^3>0\\\dfrac{2}{3}x^5y^3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^3< 0\\y^3< 0\\xy>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 0\\y< 0\end{matrix}\right.\)
18 tháng 4 2017
Hướng dẫn giải:
a) Tích của hai đơn thức 12151215 x4y2 và 5959 xy là 12151215 x4y2 . 5959 xy = 4949 x5 y3;
Đơn thức tích có bậc 8.
b) - 1717 x2y . (-2525 xy4) = 235235 x3y5;
Đơn thức tích có bậc 8.
H
18 tháng 4 2017
a) Tích của hai đơn thức \(\dfrac{12}{15}\)x4y2 và \(\dfrac{5}{9}\) xy là \(\dfrac{12}{15}\) x4y2 . \(\dfrac{5}{9}\) xy = \(\dfrac{4}{9}\) x5 y3;
Đơn thức tích có bậc 8.
b) - \(\dfrac{1}{7}\) x2y . (-\(\dfrac{2}{5}\) xy4) = \(\dfrac{2}{35}\) x3y5;
Đơn thức tích có bậc 8.
S
18 tháng 8 2017
a, \(\frac{2}{3}x=\frac{3}{4}y=\frac{4}{5}z\)
\(\Rightarrow\frac{2x}{3.12}=\frac{3y}{4.12}=\frac{4z}{5.12}\)
\(\Rightarrow\frac{x}{18}=\frac{y}{16}=\frac{z}{15}=\frac{x+y+z}{18+16+15}=\frac{45}{49}\)
Đến đây tự làm tiếp nhé
b, \(2x=3y=5z\Rightarrow\frac{2x}{30}=\frac{3y}{30}=\frac{5z}{30}\Rightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+y-z}{15+10-6}=\frac{95}{19}=5\)
=> x = 75, y = 50, z = 30
c, \(\frac{3}{4}x=\frac{5}{7}y=\frac{10}{11}z\)
\(\Rightarrow\frac{3x}{4.30}=\frac{5y}{7.30}=\frac{10z}{11.30}\)
\(\Rightarrow\frac{x}{40}=\frac{y}{42}=\frac{z}{33}\)
\(\Rightarrow\frac{2x}{80}=\frac{3y}{126}=\frac{4z}{132}=\frac{2x-3y+4z}{80-126+132}=\frac{8,6}{86}=\frac{1}{10}\)
=> x=... , y=... , z=...
d, Đặt \(\frac{x}{2}=\frac{y}{5}=k\Rightarrow x=2k,y=5k\)
Ta có: xy = 90 => 2k.5k = 90 => 10k2 = 90 => k2 = 9 => k = 3 hoặc -3
Với k = 3 => x = 6, y = 15
Với k = -3 => x = -6, y = -15
Vậy...
e, Tương tự câu d
18 tháng 8 2017
b) Ta có :\(\text{ 2x = 3y = 5z }=\frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{5}}=\frac{x+y-z}{\frac{1}{2}+\frac{1}{3}-\frac{1}{5}}=\frac{95}{\frac{19}{30}}=\frac{1}{6}\)
=> \(2x=\frac{1}{6}\Rightarrow x=\frac{1}{12}\)
\(3y=\frac{1}{6}\Rightarrow y=\frac{1}{18}\)
\(5z=\frac{1}{6}\Rightarrow z=\frac{1}{30}\)
NT
1
30 tháng 11 2017
ta có:x.y.y.z.x.z=\(\dfrac{1}{2}.\dfrac{3}{5}.\dfrac{27}{10}=\dfrac{81}{100}\)
=>(x.y.z)2= \(\left(\dfrac{9}{10}\right)^2=\left(\dfrac{-9}{10}\right)^2\)
Nếu x.y.z=\(\dfrac{9}{10}\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{1}{3}\\z=\dfrac{9}{5}\end{matrix}\right.\)
Nếu x.y.z=\(\dfrac{-9}{10}\)
=>\(\left\{{}\begin{matrix}x=\dfrac{-3}{2}\\y=\dfrac{-1}{3}\\z=\dfrac{-9}{5}\end{matrix}\right.\)
Đặt \(\dfrac{x}{5}=\dfrac{y}{2}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=5k\\y=2k\end{matrix}\right.\)\(\Rightarrow xy=10k^2\)
\(\Rightarrow k^2=1\Rightarrow k=\pm1\)
Nếu k=1 \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)
Nếu k=-1 \(\Rightarrow\left\{{}\begin{matrix}x=-5\\y=-2\end{matrix}\right.\)