Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) |x -1,7| = 2,3 => x - 1,7 = 2,3 hoặc x - 1,7 = -2,3
Với x - 1,7 = 2,3 => x = 4
Với x - 1,7 = -2,3 => x= -0,6
Vậy x = 4 hoặc x = -0,6
b) 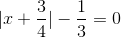 =>
=> 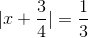
Suy ra: 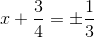
Với 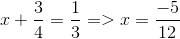
Với 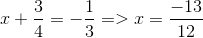
=>x-1,7=2,3 hoặc x-1,7=-2,3
=>x=2,3+1,7 hoặc x=-2,3+1,7
=>x=4 hoặc x= -0,6
vậy x=4 hoặc x=-0,6
b,\(|x+\dfrac{3}{4}|-\dfrac{1}{3}=0\)
\(|x+\dfrac{3}{4}|=\dfrac{1}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}-\dfrac{3}{4}\\x=-\dfrac{1}{3}-\dfrac{3}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
vậy x=-5/12 hoặc x= -13/12

Ix-1,7I = 2,3
TH1: x - 1,7 = 2,3
=> x = 2,3 + 1,7
=> x = 4
TH2 : x - 1,7 = -2,3
=> x = -2,3 + 1,7
=> x = -0,6
b) Ix + 3/4I - 1/3 = 0
=> Ix + 3/4I = 0 + 1/3
=> x + 3/4 = 1/3
=> x = 1/3 - 3/4
=> x = -5/12
a.
\(\left|x-1,7\right|=2,3\)
\(x-1,7=\pm2,3\)
TH1:
\(x-1,7=2,3\)
\(x=2,3+1,7\)
\(x=4\)
TH2:
\(x-1,7=-2,3\)
\(x=-2,3+1,7\)
\(x=-0,6\)
Vậy x = 4 hoặc x = -0,6
b.
\(\left|x+\frac{3}{4}\right|-\frac{1}{3}=0\)
\(\left|x+\frac{3}{4}\right|=\frac{1}{3}\)
\(x+\frac{3}{4}=\pm\frac{1}{3}\)
TH1:
\(x+\frac{3}{4}=\frac{1}{3}\)
\(x=\frac{1}{3}-\frac{3}{4}\)
\(x=\frac{4-9}{12}\)
\(x=-\frac{5}{12}\)
TH2:
\(x+\frac{3}{4}=-\frac{1}{3}\)
\(x=-\frac{1}{3}-\frac{3}{4}\)
\(x=\frac{-4-9}{12}\)
\(x=-\frac{13}{12}\)
Vậy x = -5/12 hoặc x = -13/12.

a/dễ --> tự lm
b/ \(\left(x-\dfrac{4}{7}\right)\left(1\dfrac{3}{5}+2x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{5}=0\\1\dfrac{3}{5}+2x=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\2x=\dfrac{8}{5}\Rightarrow x=\dfrac{4}{5}\end{matrix}\right.\)
Vậy...............
c/ \(\left(x-\dfrac{4}{7}\right):\left(x+\dfrac{1}{2}\right)>0\)
TH1: \(\left\{{}\begin{matrix}x-\dfrac{4}{7}>0\\x+\dfrac{1}{2}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>\dfrac{4}{7}\\x>-\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow x>\dfrac{4}{7}\)
TH2: \(\left\{{}\begin{matrix}x-\dfrac{4}{7}< 0\\x+\dfrac{1}{2}< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x< \dfrac{4}{7}\\x< -\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow x< -\dfrac{1}{2}\)
Vậy \(x>\dfrac{4}{7}\) hoặc \(x< -\dfrac{1}{2}\) thì thỏa mãn đề
d/ \(\left(2x-3\right):\left(x+1\dfrac{3}{4}\right)< 0\)
TH1: \(\left\{{}\begin{matrix}2x-3>0\\x+1\dfrac{3}{4}< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>1,5\\x< -\dfrac{7}{4}\end{matrix}\right.\)(vô lý)
TH2: \(\left\{{}\begin{matrix}2x-3< 0\\x+1\dfrac{3}{4}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x< 1,5\\x>-\dfrac{7}{4}\end{matrix}\right.\)\(\Rightarrow-\dfrac{7}{4}< x< 1,5\)
Vậy...................

a)
\(\left(3x+\dfrac{1}{3}\right)\left(x-\dfrac{1}{2}\right)=0\\ \Rightarrow\left[{}\begin{matrix}3x+\dfrac{1}{3}=0\\x-\dfrac{1}{2}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{9}\\x=\dfrac{1}{2}\end{matrix}\right.\)
b)
\(\left(x-\dfrac{3}{2}\right)\left(2x+1\right)>0\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-\dfrac{3}{2}>0\\2x+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-\dfrac{3}{2}< 0\\2x+1< 0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>\dfrac{3}{2}\\x>-\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x< \dfrac{3}{2}\\x< -\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>\dfrac{3}{2}\\x< -\dfrac{1}{2}\end{matrix}\right.\)

a) \(\left|x-1,7\right|=2,3\)
\(\Rightarrow\orbr{\begin{cases}x-1,7=2,3\\x-1,7=-2,3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=4\\x=-0,6\end{cases}}\)
b) \(\left|x+\frac{3}{4}\right|-\frac{1}{3}=0\)
\(\Rightarrow\left|x+\frac{3}{4}\right|=\frac{1}{3}\)
\(\Rightarrow\orbr{\begin{cases}x+\frac{3}{4}=\frac{1}{3}\\x+\frac{3}{4}=-\frac{1}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-\frac{5}{12}\\x=-\frac{13}{12}\end{cases}}\)

mình làm lại câu b) nha
b) |x-3|=-4
th1: x-3=-4
x=3+(-4)
x=-1
th2: x-3=4
x=3+4
x=7
b) \(\left|x-3\right|=-4\)
t/h1:\(x-3=-4\)
\(x=3-\left(-4\right)\)
\(x=7\)
t/h2:\(x-3=4\)
\(x=3-4\)
\(x=-1\)

a: \(\Leftrightarrow\left|x+\dfrac{4}{15}\right|=-2.15+3.75=1.6=\dfrac{8}{5}\)
=>x+4/15=8/5 hoặc x+4/15=-8/5
=>x=4/3 hoặc x=-28/15
c: =>x-y=0 và y+9/25=0
=>x=y=-9/25
d: =>-1/3<x-3/5<1/3
=>4/15<x<14/15
e: =>|x+5,5|>5,5
=>x+5,5>5,5 hoặc x+5,5<-5,5
=>x>0 hoặc x<-11

Bài 1:
a, \(2y.\left(y-\dfrac{1}{7}\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}2y=0\\y-\dfrac{1}{7}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=0\\y=\dfrac{1}{7}\end{matrix}\right.\)
Vậy \(y\in\left\{0;\dfrac{1}{7}\right\}\)
b, \(\dfrac{-2}{5}+\dfrac{2}{3}y+\dfrac{1}{6}y=\dfrac{-4}{15}\)
\(\Rightarrow\dfrac{5}{6}y=\dfrac{-4}{15}+\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{6}y=\dfrac{2}{15}\)
\(\Rightarrow y=\dfrac{4}{25}\)
Vậy \(y=\dfrac{4}{25}\)
Chúc bạn học tốt!!!
Bài 1:
a, \(2y\left(y-\dfrac{1}{7}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2y=0\\y-\dfrac{1}{7}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}y=0\\y=\dfrac{1}{7}\end{matrix}\right.\)
Vậy...
b, \(\dfrac{-2}{5}+\dfrac{2}{3}y+\dfrac{1}{6}y=\dfrac{-4}{15}\)
\(\Rightarrow\dfrac{5}{6}y=\dfrac{2}{15}\)
\(\Rightarrow y=\dfrac{4}{25}\)
Vậy...
Bài 2:
a, \(x\left(x-\dfrac{4}{7}\right)>0\)
\(\Rightarrow\left\{{}\begin{matrix}x>0\\x-\dfrac{4}{7}>0\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x< 0\\x-\dfrac{4}{7}< 0\end{matrix}\right.\)
\(\Rightarrow x>\dfrac{4}{7}\left(x\ne0\right)\) hoặc \(x< \dfrac{4}{7}\left(x\ne0\right)\)
Vậy...
Các phần còn lại tương tự nhé

Bài 1:
a)
\(|x+\frac{4}{15}|-|-3,75|=-|-2,15|\)
\(\Leftrightarrow |x+\frac{4}{15}|-3,75=-2,15\)
\(\Leftrightarrow |x+\frac{4}{15}|=-2,15+3,75=\frac{8}{5}\)
\(\Rightarrow \left[\begin{matrix} x+\frac{4}{15}=\frac{8}{5}\\ x+\frac{4}{15}=-\frac{8}{5}\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=\frac{4}{3}\\ x=\frac{-28}{15}\end{matrix}\right.\)
b )
\(|\frac{5}{3}x|=|-\frac{1}{6}|=\frac{1}{6}\)
\(\Rightarrow \left[\begin{matrix} \frac{5}{3}x=\frac{1}{6}\\ \frac{5}{3}x=-\frac{1}{6}\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=\frac{1}{10}\\ x=-\frac{1}{10}\end{matrix}\right.\)
c)
\(|\frac{3}{4}x-\frac{3}{4}|-\frac{3}{4}=|-\frac{3}{4}|=\frac{3}{4}\)
\(\Leftrightarrow |\frac{3}{4}x-\frac{3}{4}|=\frac{3}{2}\)
\(\Rightarrow \left[\begin{matrix} \frac{3}{4}x-\frac{3}{4}=\frac{3}{2}\\ \frac{3}{4}x-\frac{3}{4}=-\frac{3}{2}\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=3\\ x=-1\end{matrix}\right.\)
Bài 3:
a) Ta thấy:
\(|x+\frac{15}{19}|\geq 0, \forall x\Rightarrow A\ge 0-1=-1\)
Vậy GTNN của $A$ là $-1$ khi \(x+\frac{15}{19}=0\Leftrightarrow x=-\frac{15}{19}\)
b)Vì \(|x-\frac{4}{7}|\geq 0, \forall x\Rightarrow B\geq \frac{1}{2}+0=\frac{1}{2}\)
Vậy GTNN của $B$ là $\frac{1}{2}$ khi \(x-\frac{4}{7}=0\Leftrightarrow x=\frac{4}{7}\)
a) |x -1,7| = 2,3 => x - 1,7 = 2,3 hoặc x - 1,7 = -2,3
Với x - 1,7 = 2,3 => x = 4
Với x - 1,7 = -2,3 => x= -0,6
Vậy x = 4 hoặc x = -0,6
b)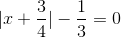 =>
=> 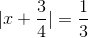
Suy ra: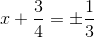
Với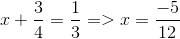
Với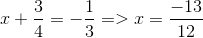
a) |x - 1,7| = 2,3 => x - 1,7 = 2,3 hoặc x - 1,7 = -2,3
Với x - 1,7 = 2,3 => x = 2,3 + 1,7 = 4
Với x - 1,7 = -2,3 => x = -2,3 + 1,7 = -0,6
Vậy x = 4 hoặc x = -0,6