Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm là \(\overline{ab}\)
Theo đề, ta có: a+b=11 và 10b+a-10a-b=27
=>a+b=11 và -9a+9b=27
=>a+b=11 và a-b=-3
=>a=4 và b=7

Tích các chữ số của số đó là số tròn chục nên trong các chữ số của số đó có chữ số \(5\)và chữ số chia hết cho \(2\).
Vì khi đổi chữ số hàng trăm và hàng đơn vị hoặc chữ số hàng nghìn và hàng chục số đó không đổi, mà số đó là số chẵn, nên chữ số hàng nghìn và hàng chục là chữ số \(5\).
Tổng hai chữ số hàng trăm và hàng đơn vị là:
\(22-5-5=12\)
Chữ sô hàng trăm và hàng đơn vị là: \(12\div2=6\).
Số cần tìm là: \(5656\).

Gọi tuổi của an là xy .
Nếu đổi chữ số hàng đơn vị và hàng chục thì ta được số mới lớn hơn số cũ 36 đơn vị nên ta có pt :
10y+x-10x-y=36 => 9y-9x=4 => x-y=-4 (1)
Tổng ba lần chữ số hàng chục và hàng đơn vị bằng 8 nên ta có pt:
3x+y=8 (2)
Từ (1) và (2) , ta có hpt:
\(\hept{\begin{cases}x-y=-4\\3x+y=8\end{cases}}\)=>\(\hept{\begin{cases}4x=4\\x-y=-4\end{cases}}\)=>\(\hept{\begin{cases}x=1\\y=5\end{cases}}\)
Vậy năm nay an 15 tuổi.

Gọi số cần tìm là \(\overline{ab}\) (0 < a < 10; 0< b < 10) => a = 2b + 2 => a - 2b = 2 (1)
Do tổng 2 chữ số là số nguyên tố nhỏ nhất có 2 chữ số => a + b = 11 (2)
Từ (1), (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}a-2b=2\\a+b=11\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}3b=9\\a+b=11\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}a=8\\b=3\end{matrix}\right.\)(tm)
Vậy số cần tìm là 83

Gọi x là chữ số hàng chục, y là chữ số hàng đơn vị.
Điều kiện: x, y ∈N*, 0 < x ≤ 9; 0 < y ≤ 9
Vì hai lần chữ số hàng chục lớn hơn 5 lần chữ số hàng đơn vị là 1 nên ta có: 2x – 5y = 1
Vì chữ số hàng chục chia cho chữ số hàng đơn vị được thương là 2 và dư cũng là 2 nên ta có: x = 2y + 2
Ta có hệ phương trình:
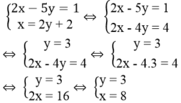
Giá trị của x và y thỏa mãn điều kiện bài toán.
Vậy số cần tìm là 83.

Gọi số cần tìm là \(\overline{xy}\)
+) Do hiệu của 3 lần chữ số hàng chục với 2 lần chữ số hàng đơn vị là 11 nên ta có phương trình \(3x-2y=11\left(1\right)\)
+) Lại có, nếu đổi chữ số hàng chục và hàng đơn vị cho nhau, ta sẽ được 1 số mới nhỏ hơn số cũ 18 đơn vị, hay
\(\overline{xy}-\overline{yx}=18\Leftrightarrow\left(10x+y\right)-\left(10y+x\right)=18\Leftrightarrow9x-9y=18\Leftrightarrow x-y=2\left(2\right)\)
Từ (1) và (2), ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-2y=11\\x-y=2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}3x-2y=11\\2x-2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=5\end{matrix}\right.\)
Vậy số cần tìm là 75
Gọi số cần tìm là \(\overline{ab}\) (0<a<10; 0<b<10) => 3a - 2b = 11 (1)
Khi đổi chỗ hai chữ số cho nhau được số mới là \(\overline{ba}\)
Do số mới nhỏ hơn số cũ 18 đơn vị => \(\overline{ab}\) - \(\overline{ba}\) = 18
⇔ 10a + b - 10b - a = 18
⇔ 9a - 9b = 18 (2)
Từ (1) và (2) ta có hệ phương trình:\(\left\{{}\begin{matrix}3a-2b=11\\9a-9b=18\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}9a-6b=33\\9a-9b=18\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}-3b=-15\\9a-9b=18\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\) (tm)
Vậy số cần tìm là 75

Gọi số đó là abc
Có a=1; b=c-2; 2b-c=4 => 2c - 4 - c=4 <=> c=8 => b=c-2=8-2=6
Vậy số đó là 186

Gọi số cần tìm là ab (a,b là chữ số ;a khác 0)
Theo đề bài a - b = 2 => a = b + 2
và ab - a2 - b2 = 1
=> 10a + b - (b + 2)2 - b2 = 1
=> 10b + 20 + b - b2 + 4b + 4 - b2 = 1
=> 15b + 24 - 2b2 = 1
=> b.(15 - 2b) = -23
=> b \(\in\) Ư(-23) = {-23; -1; 1; 23}
- Nếu b = -23 thì 15 - 2b = 61 (loại)
- Nếu b = -1 thì 15 - 2b = 17 (loại)
- Nếu b = 1 thì 15 - 2b = 13 (loại)
- Nếu b = 23 thì 15 - 2b = -31 (loại)
Vậy không tìm được số thỏa mãn đề bài
Gọi chữ số hàng đơn vị là a thì chữ số hàng chục là a + 2
Ta có số (a+2)a
Theo bài cho ta có:
=> (a+2)a = a2 + (a+2)2 + 1
=> 10(a+2) + a = a2 + a2 + 4a + 5
=> 11a + 20 = 2a2 + 4a + 5
=> 2a2 -7a+ 5 = 0
=> 2a2 - 2a - 5a + 5 = 0
=> 2a(a - 1) - 5(a - 1) = 0
=> (2a - 5)(a - 1) = 0
=> a - 1 = 0 hoặc 2a - 5 = 0
=> a = 1 (thỏa mãn) hoặc a = 5/2 (Loại)
Vậy số cần tìm là 31
19 tuổi
19 tuổi