JE
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
0
MM
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
Điều kiện: \(x\ge5\)
\(\dfrac{4\left(x-1\right)!}{4!.\left(x-5\right)!}-\dfrac{4\left(x-1\right)!}{3!\left(x-4\right)!}< \dfrac{5\left(x-2\right)!}{\left(x-4\right)!}\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-4\right)}{6}-\dfrac{2\left(x-1\right)}{3}< 5\)
\(\Leftrightarrow x^2-9x-22< 0\)
\(\Rightarrow-2< x< 11\)
\(\Rightarrow x=\left\{5;6;7;8;9;10\right\}\)
CY
0
12 tháng 3 2021
Ta có:
\(n^5+n^4-2n^3-2n^2+1=p^k\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\)
Từ giả thiết \(\Rightarrow n,k\ge2\)
Ta có:
\(\hept{\begin{cases}n^3-n-1>1,n^2+n-1>1,\forall n\ge2\\\left(n^3-n-1\right)-\left(n^2+n-1\right)=\left(n+1\right)n\left(n-2\right)\ge0,\forall n\ge2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}n^3-n-1=p^r\\n^2+n-1=p^s\end{cases}}\) trong đó \(\hept{\begin{cases}r\ge s\ge0\\r+s=k\end{cases}}\)
\(\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow n^3-n-1-\left(n-1\right)\left(n^2+n-1\right)⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\) (1)
Mặt khác :
\(\left(n^2+n-1\right)-\left(n-2\right)=n^2+1>0,\forall n\)
\(\Rightarrow n^2+n-1>n-2\ge0,\forall n\ge2\) (2)
Từ (1) và (2) => n=2 => \(p^k=25\Rightarrow\hept{\begin{cases}p=5\\k=2\end{cases}}\)
Vậy bộ số cần tìm là (n,k,p)=(2,2,5)
CM
16 tháng 11 2017
Chọn C
Phương pháp: Dễ thấy u n = u n - 1 + 6 , ∀ n ≥ 2 suy ra dãy số đã cho là cấp số cộng công sai bằng 6.
Vậy ta cần tìm số hạng đầu.
Cách giải: Ta có
log 2 u 5 + log 2 u 9 + 8 = 11
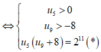
V ậ y u 1 = u 5 - 4 . 6 = 8
Do đó:
S n = u 1 + u 2 + . . + u n
= n u 1 + n ( n - 1 ) 2 d
= 3 n 2 + 5 n
⇔ 3 n 2 + 5 n - 32 > 0
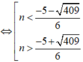
Vậy số tự nhiên n nhỏ nhất thỏa mãn S n ≥ 2 5 là 3.
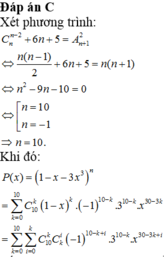
\(\Leftrightarrow\dfrac{\left(n+5\right)!}{5!.n!}=\dfrac{\left(n+3\right)!.5}{n!}\)
\(\Leftrightarrow\left(n+5\right)\left(n+4\right)=5!.5=600\)
\(\Leftrightarrow n^2+9n-580=0\Rightarrow n=20\)
☃☃