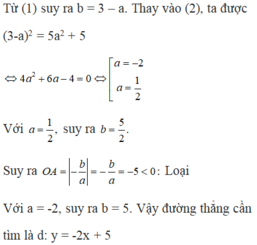Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do d qua A nên: \(a+b=3\Rightarrow b=3-a\)
Gọi B và C là giao điểm của d với Ox và Oy
\(\Rightarrow\left\{{}\begin{matrix}a.x_B+b=0\\a.0+b=y_C\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_B=-\frac{b}{a}=\frac{a-3}{a}\\y_C=b=3-a\end{matrix}\right.\)
\(\Rightarrow B\left(\frac{a-3}{a};0\right)\) ; \(C\left(0;3-a\right)\)
d cắt tia Ox và Oy \(\Rightarrow\left\{{}\begin{matrix}\frac{a-3}{a}>0\\3-a>0\end{matrix}\right.\) \(\Rightarrow a< 0\)
\(\Rightarrow OB=\frac{a-3}{a}\) ; \(OC=3-a\)
Gọi H là chân đường cao hạ từ O xuống d \(\Rightarrow OH=\sqrt{5}\)
Áp dụng hệ thức lượng trong tam giác vuông OBC
\(\frac{1}{OH^2}=\frac{1}{OB^2}+\frac{1}{OC^2}\Leftrightarrow\frac{1}{5}=\frac{a^2}{\left(a-3\right)^2}+\frac{1}{\left(3-a\right)^2}\)
\(\Leftrightarrow5\left(a^2+1\right)=\left(a-3\right)^2\)
\(\Leftrightarrow4a^2+6a-4=0\Rightarrow\left[{}\begin{matrix}a=\frac{1}{2}>0\left(l\right)\\a=-2\Rightarrow b=3-a=5\end{matrix}\right.\)
Pt đường thẳng: \(y=-2x+5\)

Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)

a: Vì (d) vuông góc với (Δ) nên -a=-1
hay a=1
Vậy: (d): y=x+b
Thay x=1 và y=-5 vào (d), ta được: b+1=-5
hay b=-6
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}5x^2+4x+3=-3x+3\\y=-3x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(5x+7\right)=0\\y=-3x+3\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(0;3\right);\left(-\dfrac{7}{5};\dfrac{36}{5}\right)\right\}\)