Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: =>2x^3-4x^2-3x^2+6x+4x-8+a+8 chia hết cho x-2
=>a+8=0
=>a=-8
b: =>2x^3+x^2-x^2-0,5x-0,5x+0,25+m-0,25 chia hết cho 2x+1
=>m-0,25=0
=>m=0,25

mk gửi cho link:
https://lazi.vn/edu/exercise/tim-n-de-da-thuc-x4-x3-6x2-x-n-chia-het-cho-da-thuc-x2-x-5

A ( x ) = x3 - 3x2 + 5x + m
= x3 - 2x2 - x2 + 2x + 3x + m
= x2 ( x - 2 ) - x ( x - 2 ) + ( 3x + m )
= ( x - 2 ) ( x2 - x ) + ( 3x + m )
Vì A chia hết cho x - 2
=> ( x - 2 ) ( x2 - x ) + ( 3x + m ) chia hết cho x - 2
mà ( x - 2 ) ( x2 - x ) chi hết cho x - 2
=> 3x + m chia hết cho x - 2
mà 3 ( x - 2 ) chia hết cho x - 2
= 3x - 6 chia hết cho x - 2
=> m = - 6
Vậy với m = - 6 thì A ( x ) = x3 - 3x2 + 5x + m chia hết cho B ( x ) = x - 2

a: \(\Leftrightarrow x^3+2x^2-3x^2-6x+5x+10+a-10⋮x+2\)
=>a-10=0
=>a=10
b: \(\Leftrightarrow x^3+x^2+x+\left(a-1\right)x^2+\left(a-1\right)x+a-1+\left(2-a\right)x+b-a+1⋮x^2+x+1\)
=>2-a=0 và b-a+1=0
=>a=2; b=a-1=2-1=1

Phân tích A = (x-3).k + một lượng ko chứa x, cho lượng này =0
(k là 1 đa thức)
Giả sử A : B = C
\(x^3-x^2-11+m=\left(x-3\right).C\)
Vì đt trên đúng với mọi x nên cho x = 3 ta có :
\(27-9-11+m=0\)
\(7+m=0\)
\(\Rightarrow m=-7\)
Vậy ............

a) đề x3+x2-x +a chia hét cho (x-1)2 ?
x3+x2-x +a=x(x2-2x+1)+3(x2-2x+1)+4x-3+a đề sai nhé
b)A(2)=0=> 8-12+10+m=0 => m=6
c)2n2-n+2=2n(n+1)-3(n+1) +5 chia het cho n+1 khi n+1 là ước của 5
n+1=-1;1;-5;5
n=-2;0;-6;4

a) \(x^3+x^2-x+a=\left(x^2-x+1\right)\left(x+2\right)+\left(a-2\right)\).
Đa thức trên chia hết cho \(x+2\) khi và chỉ khi a = 2.
b) \(x^3+ax^2+2x+b=\left(x^2+x+1\right)\left(x+1\right)+\left(a-2\right)x^2+\left(b-1\right)\) chia hết cho \(x^2+x+1\) khi và chỉ khi:
\(\frac{a-2}{1}=\frac{0}{1}=\frac{b-1}{1}\Leftrightarrow a=2;b=1\).
c) Tương tự.
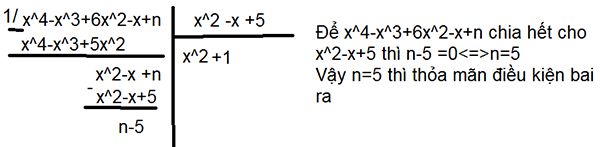

A(x) chia hết cho B(x) khi m + 6 = 0 ⇒ m= -6