L
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TV
1
12 tháng 8 2016
Ta có : \(\left(a^3+1\right)-3\left(a^2-1\right)=\left(a+1\right)\left(a^2-a+1\right)-3\left(a-1\right)\left(a+1\right)\)
\(=\left(a+1\right)\left(a^2-a+1-3a+3\right)=\left(a+1\right)\left(a^2-4a+4\right)\)
\(=\left(a+1\right)\left(a-2\right)^2\ge0\)
Do đó : \(a^3\ge3a^2-4\)
Tương tự : \(b^3\ge3b^2-4\) ; \(c^3\ge3c^2-4\)
Suy ra : \(a^3+b^3+c^3\ge3\left(a^2+b^2+c^2\right)-12=3.12-12=24\)
Min A = 24 <=> a = b = c = 2
23 tháng 4 2017
Bài giải:
a) Thế x = 4 và y = 11 vào y = 3x +b ta có: 11 = 3.4 + b ⇔ b = -1. Khi đó hàm số đã cho trở thành: y = 3x – 1. Đây là đường thẳng đi qua 2 điểm A(0;-1) và B(1/3; 0)
b) Đồ thị hàm số y = ax + 5 đi qua điểm A(-1; 3) nên: 3 = a(-1) + 5
<=> a = 2
Khi đó hàm số đã cho trở thành : y = 2x + 5. Đây là đường thẳng đi qua hai điểm A(0; 5) và B (−52;0)(−52;0)
20 tháng 10 2021
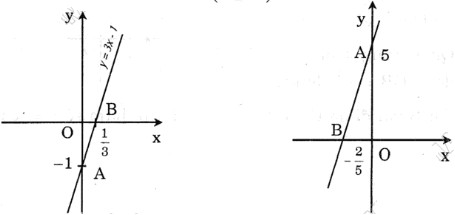
Ta có: \(4=\left(\sqrt{a}+1\right)\left(\sqrt{b}+1\right)=\sqrt{ab}+\sqrt{a}+\sqrt{b}+1\)
\(\le\frac{a+b}{2}+\frac{a+1}{2}+\frac{b+1}{2}+1\Rightarrow a+b\ge2\)
Do đó \(P=\frac{a^2}{b}+\frac{b^2}{a}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\ge2\)
Dấu bằng xảy ra khi a = b = 1
VI
1
21 tháng 12 2016
Bài này lớp 6 làm còn được.
\(0\le a^2,b^4\le1\Rightarrow\orbr{\begin{cases}a^2=0,b^4=1\\a^2=1,b^4=0\end{cases}}\)
Trường hợp 1: \(a^2=0\Rightarrow a=0\). Từ giả thiết thứ 2 suy ra \(b=1\). Thử lại thấy thoả.
Trường hợp 2: \(b^4=0\Rightarrow b=0\). Từ giả thiết 2 suy ra \(a=1\) hoặc \(a=-1\). Thử lại thấy cả 2 cùng thoả.
HF
3 tháng 8 2020
\(\frac{1}{a}+\frac{1}{b}-\left(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}\right)^2=\frac{1}{a}+\frac{1}{b}-\frac{a}{b}-\frac{b}{a}+2=\frac{a+b-1}{ab}+2\)
\(\frac{2\left(a+b-1\right)}{\left(a+b\right)^2-1}+2=\frac{2}{a+b+1}+2\ge\frac{2}{\sqrt{2\left(a^2+b^2\right)}+1}+2=\frac{2}{\sqrt{2}+1}+2=2\sqrt{2}\)
Dấu = xảy ra khi \(a=b=\frac{1}{\sqrt{2}}\)
T
3 tháng 8 2020
Đặt \(a=\frac{x^2}{z},b=\frac{y^2}{z}\rightarrow x^4+y^4=z^2\) where x, y, z> 0
\(z\left(\frac{1}{x^2}+\frac{1}{y^2}\right)-\left(\frac{x}{y}-\frac{y}{x}\right)^2\ge2\sqrt{2}\)
\(\Leftrightarrow\sqrt{x^4+y^4}\left(\frac{1}{x^2}+\frac{1}{y^2}\right)\ge2\sqrt{2}+\left(\frac{x}{y}-\frac{y}{x}\right)^2\)
\(\Leftrightarrow\frac{2\left(3-2\sqrt{2}\right)\left(x^2-y^2\right)^2}{x^2y^2}\ge0\) *Đúng*
a2-b2=11
<=>(a-b)(a+b)=11
Mà a+b=12
=> a-b=11/12
Vào MTCT bấm MODE 5 1 (giải hệ phương trình bậc nhất 2 ẩn)
Gõ lần lượt các hệ số
1=1=12
1=-1=11/12
=...
a=155/24
b=133/24
Vậy a=155/24 và b=133/24