
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Làm sai thì thôi nha!
ĐK: x>=0 \(A=x-2.\sqrt{x}.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\)
\(=\left(\sqrt{x}-\frac{1}{2}\right)^2-\frac{1}{4}\ge-\frac{1}{4}\)
đẳng thức xảy ra khi x = 1/4
A=\(x-\sqrt{x}=x-2\times\sqrt{x}\times\frac{1}{2}+\frac{1}{4}-\frac{1}{4}=(\sqrt{x}-\frac{1}{2})^2+\frac{1}{4}\ge\frac{1}{4}\)
GTNN A=\(\frac{1}{4}\Leftrightarrow\sqrt{x}-\frac{1}{2}=0\Leftrightarrow\sqrt{x}=\frac{1}{2}\Leftrightarrow x=\frac{1}{4}\)


\(x^3_1-x_2^3=\left(\left(x_1-x_2\right)\left(x^2_1+x_1x_2+x_2^2\right)=\left(x_1-x_2\right)\left[\left(x_1+x_2\right)\right]^2-x_1x_2=......\right)\)

a/ Bạn tự giải
b/ \(\left\{{}\begin{matrix}a=1\\c=-3\end{matrix}\right.\) \(\Rightarrow ac=-3< 0\Rightarrow\) phương trình luôn có 2 nghiệm pb trái dấu với mọi giá trị của m
c/ Theo Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=-2\left(m+1\right)\\x_2x_2=-3\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1^2+x_2^2+2x_1x_2-2x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=4\left(m+1\right)^2+6=4m^2+8m+10\)
\(\frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{x_1x_2}=\frac{-2\left(m+1\right)}{-3}=\frac{2}{3}m+\frac{2}{3}\)
\(\Delta'=\left(m+1\right)^2+3>0\) \(\forall m\Rightarrow\) pt luôn có 2 nghiệm pb
Cách nào cũng như nhau thôi

\(đkcđ\Leftrightarrow x\ge0\)
\(B=\frac{x+5}{\sqrt{x}+2}=\frac{x-4+9}{\sqrt{x}+2}=\frac{x-4}{\sqrt{x}+2}+\frac{9}{\sqrt{x}+2}.\)
\(=\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}+\frac{9}{\sqrt{x}+2}=\sqrt{x}-2+\frac{9}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\frac{9}{\sqrt{x}+2}-4\)
Áp dụng bđt Cô - si cho hai số dương \(\sqrt{x}+2\)và \(\frac{9}{\sqrt{x}+2}\), ta có :
\(\sqrt{x}+2+\frac{9}{\sqrt{x}+2}\ge2\sqrt{\frac{\left(\sqrt{x}+2\right).9}{\sqrt{x}+2}}\)
\(\Rightarrow\sqrt{x}+2+\frac{9}{\sqrt{x}+2}\ge2.3\)
\(\Rightarrow\sqrt{x}+2+\frac{9}{\sqrt{x}+2}-4\ge6-4\)
\(\Rightarrow\sqrt{x}+2+\frac{9}{\sqrt{x}+2}-4\ge2\)
Hay \(B_{min}=2\)\(\Leftrightarrow\sqrt{x}+2=\frac{9}{\sqrt{x}+2}\)
\(\Rightarrow\sqrt{x}+2-\frac{9}{\sqrt{x}+2}=0\)
\(\Rightarrow\frac{\left(\sqrt{x}+2\right)^2-9}{\sqrt{x}+2}=0\)
\(\Rightarrow\left(\sqrt{x}+2\right)^2-3^2=0\)
\(\Rightarrow\left(\sqrt{x}+2-3\right)\left(\sqrt{x}+2+3\right)=0\)
\(\Rightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}+5\right)=0\)
Vì \(\sqrt{x}+5>0\Rightarrow\sqrt{x}-1=0\)
\(\Rightarrow\sqrt{x}=1\Rightarrow x=1\)
\(KL:B_{min}=2\Leftrightarrow x=1\)


a, ĐKXĐ : \(\left\{{}\begin{matrix}\dfrac{3x-5}{x-1}\ge0\\x-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3x-5\ge0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}3x-5\le0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge\dfrac{5}{3}\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{5}{3}\\x< 1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{5}{3}\\x< 1\end{matrix}\right.\)
Vậy ...
b, Ta có : \(A=\sqrt{\dfrac{3x-5}{x-1}}=3\)
\(\Leftrightarrow3x-5=9x-9\)
\(\Leftrightarrow x=\dfrac{2}{3}\left(TM\right)\)
Vậy ...
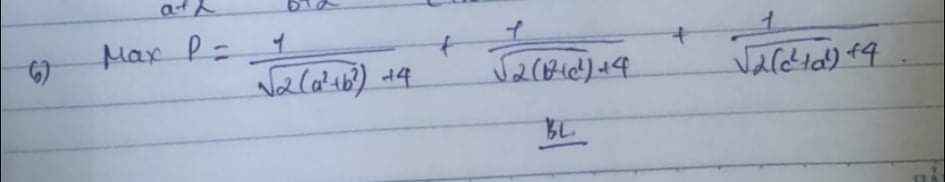 mọi người giúp em với ạ😁😁😁
mọi người giúp em với ạ😁😁😁
\(A=x-\sqrt{x}\) \(\left(ĐKXĐ:x\ge0\right)\)
\(A=x-2.\sqrt{x}.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\)
\(A=\left(x-\frac{1}{2}\right)^2\) \(-\frac{1}{4}\)
Có \(\left(x-\frac{1}{2^2}\right)\ge0\forall x\ge0\)
\(\left(x-\frac{1}{2}\right)^2\) - 1/4 >= \(\frac{-1}{4}\)mọi x>=0
Dấu = sảy ra \(\Leftrightarrow\) x- \(\frac{1}{2}\) = 0
\(\Leftrightarrow\) x = 1 / 2 ( t/m )
vậy A đạt GTNN là -1/4 tại x = 1/2
Tớ nhầm nhé \(x\) từ dòng thứ 3 xuống pahir thay =\(\sqrt{x}\)