Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
\(A=11\dfrac{3}{13}-5\dfrac{3}{13}-2\dfrac{4}{7}\)
\(A=6-2\dfrac{4}{7}\)
\(A=5\dfrac{7}{7}-2\dfrac{4}{7}\)
\(A=3\dfrac{3}{7}\)
\(B=\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(B=\left(6\dfrac{4}{9}-4\dfrac{4}{9}\right)+3\dfrac{7}{11}\)
\(B=2+3\dfrac{7}{11}\)
\(B=5\dfrac{7}{11}\)
\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+1\right)-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\dfrac{13}{11}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-65}{77}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{4}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{160}{11}\)
\(D=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(D=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{375}{1000}.\dfrac{5}{28}\)
\(D=\dfrac{7}{28}=\dfrac{5}{2}\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{12}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right).0\)
\(\Rightarrow E=0\)

tìm x a)
\(\dfrac{7}{2}\)-\(\left(x+\dfrac{7}{10}\right)\): \(\dfrac{6}{5}\) = \(\dfrac{-5}{4}\)
\(\left(x+\dfrac{7}{10}\right)\): \(\dfrac{6}{5}\) = \(\dfrac{-5}{4}\) + \(\dfrac{7}{2}\)
\(\left(x+\dfrac{7}{10}\right)\): \(\dfrac{6}{5}\) = \(\dfrac{-5}{12}+\dfrac{7}{12}\)
\(\left(x+\dfrac{7}{10}\right)\): \(\dfrac{6}{5}\) = \(\dfrac{-12}{12}=1\)
\(x+\dfrac{7}{10}\)= 1 . \(\dfrac{6}{5}\)
*Rồi tự làm phần tt đi

a: \(=\dfrac{4\cdot2+4\cdot9}{55}+\dfrac{5}{6}=\dfrac{4}{5}+\dfrac{5}{6}=\dfrac{49}{30}\)
b: \(=\dfrac{3}{2}\cdot\dfrac{3}{5}-\left(\dfrac{3}{7}+\dfrac{3}{20}\right)\cdot\dfrac{10}{3}\)
\(=\dfrac{9}{10}-\dfrac{81}{140}\cdot\dfrac{10}{3}\)
\(=\dfrac{9}{10}-\dfrac{27}{14}=\dfrac{-36}{35}\)
c: \(=15+\dfrac{3}{13}-3-\dfrac{4}{7}-8-\dfrac{3}{13}\)
\(=4-\dfrac{4}{7}=\dfrac{24}{7}\)
d: \(=\dfrac{-7}{9}\left(\dfrac{4}{11}+\dfrac{7}{11}\right)+5+\dfrac{7}{9}=5\)

a) \(49\dfrac{8}{23}-\left(5\dfrac{7}{32}+14\dfrac{8}{23}\right)\)
\(=\dfrac{1135}{23}-\left(\left(5+14\right)+\left(\dfrac{7}{32}+\dfrac{8}{23}\right)\right)\)
\(=\dfrac{1135}{23}-\left(19+\dfrac{417}{736}\right)\)
\(=\dfrac{1135}{23}-19\dfrac{417}{736}\)
\(=\dfrac{1135}{23}-\dfrac{14401}{736}\)
\(=\dfrac{953}{32}\)
b) \(-\dfrac{3}{7}\cdot\dfrac{5}{9}+\dfrac{4}{9}\cdot\dfrac{-3}{7}+2\dfrac{3}{7}\)
\(=-\dfrac{1}{7}\cdot\dfrac{5}{3}-\dfrac{4}{3}\cdot\dfrac{1}{7}+\dfrac{17}{7}\)
\(=-\dfrac{5}{21}-\dfrac{4}{21}+\dfrac{17}{7}\)
\(=2\)
c) \(0,7\cdot2\dfrac{2}{3}\cdot20\cdot0,375\cdot\dfrac{5}{28}\)
\(=\dfrac{7}{10}\cdot\dfrac{8}{3}\cdot20\cdot\dfrac{3}{8}\cdot\dfrac{5}{28}\)
\(=2\cdot\dfrac{5}{4}\)
\(=\dfrac{5}{2}\)
d) \(\left(9\dfrac{30303}{80808}+7\dfrac{303030}{484848}\right)+4,03\)
\(=\left(9\cdot\dfrac{3}{8}+\dfrac{303030}{69264}\right)+\dfrac{403}{100}\)
\(=\left(\dfrac{27}{8}+\dfrac{35}{8}\right)+\dfrac{403}{100}\)
\(=\dfrac{31}{4}+\dfrac{403}{100}\)
\(=\dfrac{589}{50}\)
P/s: Đánh dấu phẩy, dấu chấm (dấu nhân) cần rõ ràng (vì dấu chấm người ta sẽ hiểu là dấu nhân thay vì hiểu là dấu phẩy)
a) \(49\dfrac{8}{23}\)- \(\left(5\dfrac{7}{32}+14\dfrac{8}{23}\right)\)
= \(\left(49\dfrac{8}{23}-14\dfrac{8}{23}\right)+5\dfrac{7}{32}\)
=35+\(5\dfrac{7}{32}\)
=\(\dfrac{1287}{32}\)
b)\(-\dfrac{3}{7}.\dfrac{5}{9}+\dfrac{4}{9}.\dfrac{-3}{7}+2\dfrac{3}{7}\)
=\(\left[\left(\dfrac{-3}{7}\right).\left(\dfrac{5}{9}+\dfrac{4}{9}\right)\right]+2\dfrac{3}{7}\)
=\(\left[\left(\dfrac{-3}{7}\right).\dfrac{9}{9}\right]+2\dfrac{3}{7}\)
=\(\left[\left(\dfrac{-3}{7}\right).1\right]+2\dfrac{3}{7}\)
=\(\left(\dfrac{-3}{7}\right)+2\dfrac{3}{7}\)
=2
c) 0,7.\(2\dfrac{2}{3}\).20.0.375.\(\dfrac{5}{28}\)
=0 (Vì có một thừ số là 0 nên nguyên cả tích là 0)
d)\(\left(9\dfrac{30303}{80808}+7\dfrac{303030}{484848}\right)+4,03\)
=17+4,03
=21,03

B1: Tính nhanh:
\(E=\dfrac{-9}{10}\cdot\dfrac{5}{14}+\dfrac{1}{10}\cdot\dfrac{-9}{2}+\dfrac{1}{7}\cdot\dfrac{-9}{10}\)
\(E=\dfrac{-9}{10}\cdot\dfrac{5}{14}+\dfrac{-9}{10}\cdot\dfrac{1}{2}+\dfrac{1}{7}\cdot\dfrac{-9}{10}\)
\(E=\dfrac{-9}{10}\cdot\left(\dfrac{5}{14}+\dfrac{1}{2}+\dfrac{1}{7}\right)\)
\(E=\dfrac{-9}{10}\cdot\left(\dfrac{5}{14}+\dfrac{7}{14}+\dfrac{2}{14}\right)\)
\(E=\dfrac{-9}{10}\cdot1=\dfrac{-9}{10}\)
B2: Chứng tỏ rằng:
\(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}< 1\)
Ta có: \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\)
\(\Leftrightarrow1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(\Leftrightarrow1-\dfrac{1}{100}=\dfrac{99}{100}\)
Mà \(\dfrac{99}{100}< 1\)
\(\Rightarrow\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}< 1\)
Tick mình nha!![]()

Ta có : \(\dfrac{7}{9}.\left(1\dfrac{1}{6}-1:1\dfrac{1}{19}-\dfrac{1}{15}\right)+4\dfrac{2}{5}:24\)
\(=\dfrac{7}{9}.\left(\dfrac{7}{6}-\dfrac{19}{20}-\dfrac{1}{15}\right)+\dfrac{22}{5}.\dfrac{1}{24}\)
=\(\dfrac{7}{9}.\left(\dfrac{70}{60}-\dfrac{57}{60}-\dfrac{4}{60}\right)+\dfrac{11}{60}\)
\(=\dfrac{7}{9}.\dfrac{3}{20}+\dfrac{11}{60}\)
\(=\dfrac{7}{60}+\dfrac{11}{60}=\dfrac{18}{60}=\dfrac{3}{10}\)

A,
\(\left(7\dfrac{4}{9}+3\dfrac{7}{11}\right)-3\dfrac{4}{9}=7\dfrac{4}{9}+3\dfrac{7}{11}-3\dfrac{4}{9}\)
\(=7\dfrac{4}{9}-3\dfrac{4}{9}+3\dfrac{7}{11}=4+3\dfrac{7}{11}=7\dfrac{7}{11}\)
B,
\(5\dfrac{2}{7}.\dfrac{8}{11}+5\dfrac{2}{7}.\dfrac{5}{11}-5\dfrac{2}{7}.\dfrac{2}{11}=5\dfrac{2}{7}.\left(\dfrac{8}{11}+\dfrac{5}{11}-\dfrac{2}{11}\right)\)
\(=5\dfrac{2}{7}.1=5\dfrac{2}{7}\)
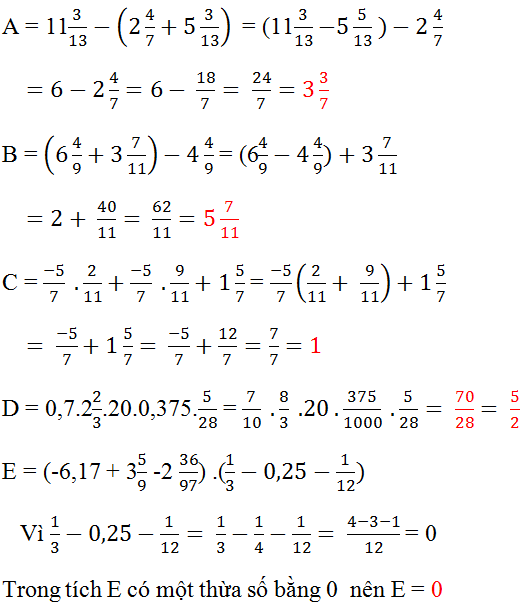
a)\(\dfrac{-2}{9}>\dfrac{-7}{9}\)
b)\(\dfrac{5}{7}>\dfrac{-10}{7}\)