Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tâm O của đường tròn nội tiếp tam giác đều cũng là giao điểm ba đường trung tuyến, ba đường cao.
Do đó đường cao h=AE=3.OE=3cm.
Trong tam giác đều, h = a√3/2 (a là độ dài mỗi cạnh).
Suy ra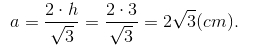 
Do đó diện tích tam giác ABC là
Ta chọn (D).
Chọn phương án (B)
Tam giác đều ABC nội tiếp đường tròn tâm O bán kính R. Khi đó \(\widehat{BOC}\) có số đo bằng \(120^0\)
Gọi cạnh huyền là a, cạnh đối diện góc 300 là c, cạnh còn lại là b
Tính được \(b=c.\cot30=c\sqrt{3}\) nên \(a=\sqrt{b^2+c^2}=\sqrt{\left(c\sqrt{3}\right)^2+c^2}=2c\)
Bán kính đường tròn ngoại tiếp là R = a/2 = 2c/2 = c
Bán kính đường tròn nội tiếp là
\(r=\frac{S}{p}=\frac{bc}{2p}=\frac{bc}{a+b+c}=\frac{c^2\sqrt{3}}{2c+c\sqrt{3}+c}=\frac{c^2\sqrt{3}}{\left(3+\sqrt{3}\right)c}=\frac{\left(\sqrt{3}-1\right)c}{2}\)
Do đó \(\frac{R}{r}=c.\frac{2}{\left(\sqrt{3}-1\right)c}=1+\sqrt{3}\)
bạn thi vio à kết bạn vs mk nhé
Gọi A; B; CD,E,F làn lượt là tiếp điểm của đường tròn nội tiếp tam giác với BC; CA; AB
Khi đó: \(S=S_{BIC}+S_{CAI}+S_{BAI}=\frac{1}{2}\) \(BC.ID+CA.IE+AB.IF=p.r\)
\(\frac{S}{h_a}+\frac{S}{h_b}+\frac{S}{h_c}=\frac{1}{2}\) \(a+b+c=p=\frac{S}{r}\)
\(\RightarrowĐPCM\)
Không tính tổng quát, giả sử: \(h_a\le h_b\le h_c\)
\(\Rightarrow\frac{1}{h_a}\ge\frac{1}{h_b}\ge\frac{1}{h_c}\)
\(\Rightarrow\frac{1}{h_a}\ge\frac{1}{3}\)
\(\Rightarrow h_a\le3\)
Mặt khác: \(\frac{1}{h_a}< \frac{1}{r}=1\Rightarrow h_a>1\Rightarrow h_a\ge2\)
Vậy: \(h_a=2\)hoặc \(h_a=3\)
Nếu \(h_a=2\)
\(\frac{1}{h_b}+\frac{1}{h_c}=1-\frac{1}{2}=\frac{1}{2}\)**
Ta có: \(a\ge b\ge c\)do \(h_a\le h_b\le h_c\)
Để a; b; clà 3 cạnh của một hình tam giác ta chỉ cần b + c > a do khi \(a\ge b\ge c\)theo ta sẽ có ngay a + c > b, a + b > c
\(\Leftrightarrow\frac{S}{h_b}+\frac{S}{h_c}>\frac{S}{h_a}\)
\(\Leftrightarrow\frac{1}{h_b}+\frac{1}{h_c}>\frac{1}{h_a}=\frac{1}{2}\)mâu thuẫn với **
Vậy, loại trường hợp này.
\(\Rightarrow h_a=3\Rightarrow h_b\ge h_c\ge3\)
\(\frac{1}{h_b}+\frac{1}{h_c}=1-\frac{1}{3}=\frac{2}{3}\)
\(\frac{1}{h_b}\ge\frac{1}{h_c}\)
Suy ra: \(\frac{1}{h_b}\ge\frac{1}{3}\Rightarrow h_b\le3\)
Mà: \(h_b\ge\frac{1}{3}\Rightarrow h_b\le3\)
Vậy: \(h_b=3\Rightarrow h_c=3\)
\(\RightarrowĐPCM\)
(C)
Giải:
Tỉ số bán kính đường tròn nội tiếp và đường tròn ngoại tiếp một tam giác đều bằng
(A) \(\dfrac{1}{3}\) (B) \(\dfrac{1}{2}\) (C) \(\dfrac{1}{\sqrt{2}}\) (D) 2