Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Những đường thẳng song song với mặt phẳng (ABKI) là A’B’; D’C’; DC; GH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') mà A’D’ nằm trong mặt phẳng (A’D’C’B’) nên (A'B'C'D') ⊥ (CDD'C')

Tham khảo:
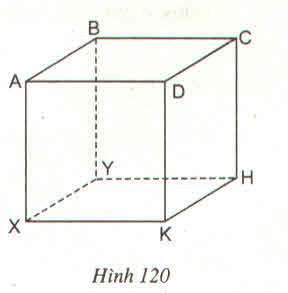
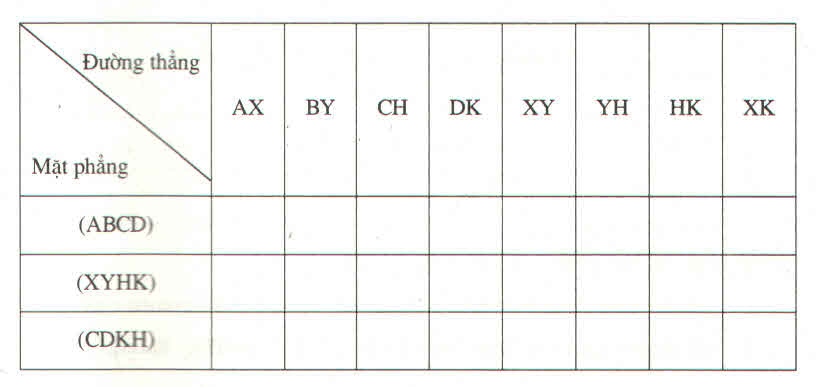
a. Những cặp mặt phẳng song song với nhau là:
mp (ABCD) và mp (XYHK)
mp (ADKX) và mp (BCHY)
mp (ABYX) và mp (CDKH)
b. Những cặp mặt phẳng vuông góc với nhau là:
mp (ABCD) và mp (ADKX); mp (XYHK) và mp (ADKX)
mp (ABCD) và mp (ABYX); mp (XYHK) và mp (ABYX)
mp (ABCD) và mp (BCHY); mp (XYHK) và mp (BCHY)
mp (ABCD) và mp (CDKH); mp (XYHK) và mp (CDKH)
mp (ADKX) và mp (CDKH); mp (ADKX) và mp (ABYX)
mp (BCHY) và mp (CDKH); mp (BCHY) và mp (ABYX)
c. Hai mặt phẳng (BCHY) và (KXYH) vuông góc với nhau.
d: 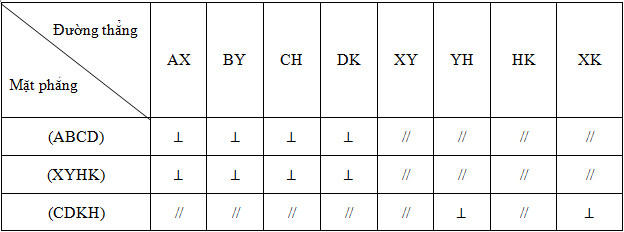

c) Mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).
a) Ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD.
b) Cạnh CD song song với hai mặt phẳng (ABEF) và (EFGH).
c) Mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

Lời giải
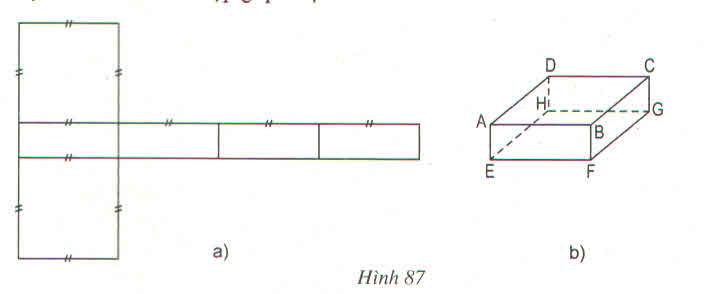
1. Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và (DHEA)
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) tại H.
1. Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và (DHEA)
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) tại H.

a. Ba đường thẳng CG, HG, FG cắt nhau tại G.
b. Mặt phẳng (ABFE) và mặt phẳng (BCGF) cắt nhau theo đường thẳng BF.
c. Mặt phẳng (EFBA) và mặt phẳng (FGCB) cắt nhau theo đường thẳng BF.

a. Ta có: A1B1 // mp(ABCD)
A1B1 // mp(CDD1C1)
b. Ta có: AC // A1C1
Suy ra: AC không thuộc mp(A1B1C1)

a: \(mp\left(EFGH\right);mp\left(ABCD\right)\)
\(mp\left(ABFE\right);mp\left(CDHG\right)\)
\(mp\left(ADHE\right);mp\left(BCGF\right)\)
b: Các điểm D,H,G,C cùng thuộc mặt phẳng CDHG
c: Các điểm D,H,G,F không thuộc cùng một mặt phẳng
d: A,B,G,H cùng thuộc mặt phẳng ABGH

a) Những đường thẳng song song với mặt phẳng (EFGH) là: AB; BC; CD; DA.
b) Đường thẳn AB song song với những mặt phẳng: (CDHG); (EFGH); (DCFE)
c) Đường thẳng AD song song với những đường thẳng: BC, FG, EH
a) Những đường thẳng song song với mặt phẳng (EFGH) là: AB; BC; CD; DA.
b) Đường thẳn AB song song với những mặt phẳng: (CDHG); (EFGH); (DCFE)
c) Đường thẳng AD song song với những đường thẳng: BC, FG, EH
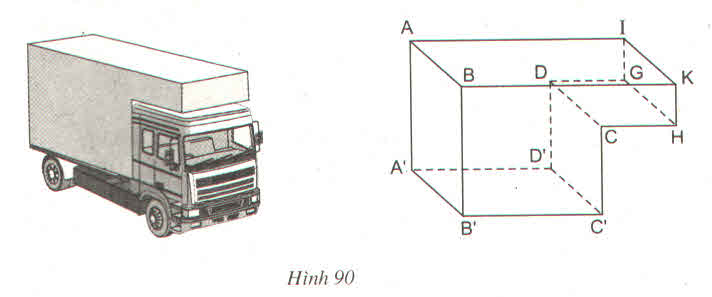





a) Những đường thẳng song song với mặt phẳng (ABKI) là DG; CH; A'D'; B'C'; A'B'; D'C'; DC; JH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') => (A'B'C'D') \(\perp\) (CDD'C')
a) Những đường thẳng song song với mặt phẳng (ABKI) là : A’B’; D’C’; DC; JH
b) Những đường thẳng vuông góc với mặt phẳng (DCC’D’) là : A’D’; B’C’DJ; CH; AI; BK
c) Hai mặt phẳng (A’B’C’D’) và (CDD’C’) vuông góc với nhau