Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(3x^2\left(2x^3-x+5\right)\)
\(=3x^2\cdot2x^3-3x^2\cdot x+5\cdot3x^2\)
\(=6x^5-3x^3+15x^2\)
b: \(x^2y\left(4xy+3y-5x\right)\)
\(=x^2y\cdot4xy+x^2y\cdot3y-x^2y\cdot5x\)
\(=4x^3y^2+3x^2y^2-5x^3y\)

a,A=3x^2y^4+5x^3+xy-3x^2y^4
A=5x3 +xy
=> bậc của A là 3
b,B=7x^3y.(-4x^2y^2)+17x^2y^3-4x^2y+28x^2y^4
=> bậc của B là 8
c,C=5x^4y^2-7x^3y^2.(-2xy^2)-5x^4y^2+x^3-14x^4y^4
C = 5x4y2 -7x3y2 (-2xy2) - 5x4y2 +x3 -14x4y4
C = 5x4y2 + 14x4y4 -5x4y2 +x3 -14x4y4
C = x3
=> Bậc của C là 3

Ta có :\(15x=10y=6z\Rightarrow\hept{\begin{cases}15x=10y\\10y=6z\end{cases}}\Rightarrow\hept{\begin{cases}3x=2y\\5y=3z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{2}=\frac{y}{3}\\\frac{y}{3}=\frac{z}{5}\end{cases}}\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)
Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=k\Rightarrow\hept{\begin{cases}x=2k\\y=3k\\z=5k\end{cases}}\)
Khi đó 5x3 + 2y3 - z3 = 31
=> 5(2k)3 + 2(3k)3 - (5k)3 = 31
=> 40k3 + 54k3 - 125k3 = 31
=> -31k3 = 31
=> k3 = -1
=> k = -1
=> x = -2 ; y = -3 ; z = -5
b) Ta có 7x = 14y = 6z => \(\hept{\begin{cases}7x=14y\\14y=6z\end{cases}}\Rightarrow\hept{\begin{cases}x=2y\\7y=3z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{2}=\frac{y}{1}\\\frac{y}{3}=\frac{z}{7}\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{6}=\frac{y}{3}\\\frac{y}{3}=\frac{z}{7}\end{cases}}\Rightarrow\frac{x}{6}=\frac{y}{3}=\frac{z}{7}\)
Đặt \(\frac{x}{6}=\frac{y}{3}=\frac{z}{7}=k\Rightarrow\hept{\begin{cases}x=6k\\y=3k\\z=7k\end{cases}}\)
Khi đó 2x2 - 3y2 = 5
<=> 2.(6k)2 - 3.(3k)2 = 5
=> 72k2 - 27k2 = 5
=> 45k2 = 5
=> k2 = 1/9
=> k = \(\pm\frac{1}{3}\)
Nếu k = 1/3 => x = 2 ; y = 1 ; z = 7/3
Nếu k = -1/3 => x = -2 ; y = - 1 ; z = -7/3
Vậy các cặp (x;y;z) thỏa mãn là : (2;1;7/3) ; (-2 ; - 1; -7/3)
c) Ta có : \(3x=8y=5z\Rightarrow\frac{3x}{120}=\frac{8y}{120}=\frac{5z}{120}\Rightarrow\frac{x}{40}=\frac{y}{15}=\frac{z}{24}\)
Đặt \(\frac{x}{40}=\frac{y}{15}=\frac{z}{24}=k\Rightarrow\hept{\begin{cases}x=40k\\y=15k\\z=24k\end{cases}}\)
Khi đó |x - 2y| = 5
<=> |40k - 2.15k| = 5
=> |10k| = 5
=> \(\orbr{\begin{cases}10k=5\\10k=-5\end{cases}}\Rightarrow\orbr{\begin{cases}k=\frac{1}{2}\\k=-\frac{1}{2}\end{cases}}\)
Nếu k = 5 => x = 20 ; y = 7,5 ; z = 12
Nếu k = -5 => x = -20 ; y =-7,5 ; z = -12
d) 4x = 5y = 6z => \(\frac{4x}{60}=\frac{5y}{60}=\frac{6z}{60}\Rightarrow\frac{x}{15}=\frac{y}{12}=\frac{z}{10}\)
Đặt \(\frac{x}{15}=\frac{y}{12}=\frac{z}{10}=k\Rightarrow\hept{\begin{cases}x=15k\\y=12k\\z=10k\end{cases}}\)
Khi đó (3x - 2y)2 = 16
<=> (3.15k - 2.12k)2 = 16
=> (45k -24k)2 = 16
=> (21k)2 = 16
=> \(\orbr{\begin{cases}21k=4\\21k=-4\end{cases}}\Rightarrow\orbr{\begin{cases}k=\frac{4}{21}\\k=-\frac{4}{21}\end{cases}}\)
Nếu k = 4/21 => x = 20/7 ; y = 16/7 ; z = 40/21
Nếu k = -4/21 => x = -20/7 ; y = -16/7 ; z = -40/21

A)\(5xyz.4x^2y^2.\left(-2x^3y\right)=\left(5.4.\left(-2\right)\right).\left(xx^2x^3\right).\left(yy^2y\right)=\left(-40\right)x^6y^4\)
- BẬC : 10
- HỆ SỐ: -40
B) \(-xy.\left(\frac{1}{2}x^3y^4\right).\left(\frac{-4}{7}x^2y^5\right)=\left(\frac{1}{2}.\frac{-4}{7}.\left(-1\right)\right).\left(xx^3x^2\right).\left(y^4y^5y\right)=\frac{2}{7}x^6y^{10}\)
- BẬC : 16
- HỆ SỐ: 2/7
C) \(\frac{5}{3}x^2y^4.\left(\frac{-6}{5}xy^3\right).\left(-xy\right)=\left(\frac{5}{3}.\frac{-6}{5}.\left(-1\right)\right).\left(x^2xx\right).\left(y^4y^3y\right)=2x^4y^8\)
- BẬC : 12
- HỆ SỐ : 2
D) \(\left(\frac{-1}{3}x^2y^5\right).\left(\frac{3}{4}xy\right).5x=\left(\frac{-1}{3}.\frac{3}{4}.5\right).\left(x^2xx\right).\left(y^5y\right)=\frac{-5}{4}x^4y^6\)
- BẬC : 10
- HỆ SỐ : -5 /4
CHÚC BN HỌC TỐT!!

\(3x^2y^3-A-5x^3y^2+B=8x^2y^3-4x^3y^2\)
\(\Leftrightarrow-A+B=5x^2y^3+x^3y^2\)
\(-6x^2y^3+C-3x^3y^2-D=2x^2y^3-7x^3y^2\)
\(\Leftrightarrow C-D=8x^2y^3-4x^3y^2\)
Do \(A\) và \(C\) đồng dạng nên \(A=-5x^2y^3,C=8x^2y^3\) suy ra \(B=x^3y^2,D=4x^3y^2\) hoặc \(A=-x^3y^2,C=-4x^3y^2\) suy ra \(B=5x^2y^3,D=-8x^2y^3\).
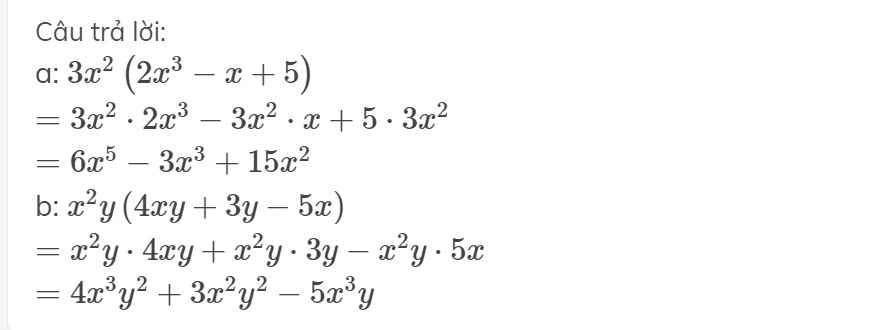
Answer:
\(3x^2.\left(2x^3-x+5\right)\)
\(=3x^2.2x^3+3x^2.(-x)+3x^2.5\)
\(=6x^5-3x^3+15x^2\)
\((4xy+3y-5x).x^2y\)
\(=4xy.x^2y+3y.x^2y-5x.x^2y\)
\(=4x^3+3x^2y^2-5x^3y\)