Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

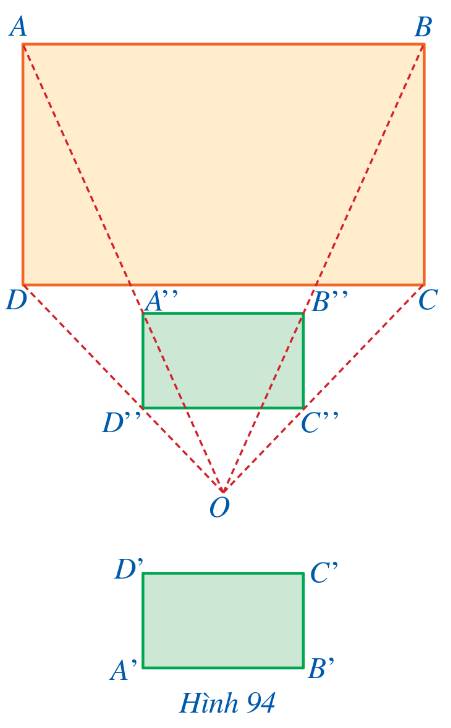
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau

a, Dễ CM AEOF là hình chữ nhật vì có 3 góc vuông
=>AO=EF
Mà AO=OC=AC/2 (O là tr.điểm AC do ABCD là hình chữ nhật)
=>EF=AC/2=12/2=6cm
b) CM \(\Delta AHO=\Delta CKO\left(ch-gn\right)\) => AH=KC
Mà AH//KC (cùng vuông góc với BD)
=>AHCK là hình bình hành => AK//HC
c, Có OA=OB=OC=OD (do ABCD là hình chữ nhật)
tam giác OAD cân có OE là đg cao nên cũng là trung tuyến => F là tr.điểm AD
Xét tam giác AHD vuông ở H có F là tr.điểm AD nên HF là trung tuyến ứng với cạnh huyền AD => HF=AF (=1/2AH)
Mà AF=OE (AEOF là hình chữ nhật)
=>HF=OE
Dễ CM EF là đg trung bình của tam giác ABD => EF//BD hay EF//OH=>EFHO là hình thang,mà HF=OE
=>EFHO là hình thang cân

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
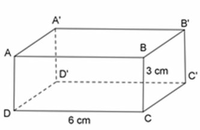
Thực hiện theo hướng dẫn của GV và SGK.