
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
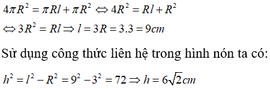

Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:
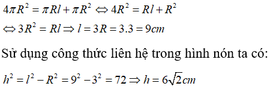

Gọi chiều cao của hình nón là x
Độ dài đường sinh là \(\sqrt{x^2+25}\)
Diện tích xung quanh là:
\(pi\cdot x\cdot\sqrt{x^2+25}\)
Thể tích là: \(pi\cdot x\cdot5^2=pi\cdot x\cdot25\)
Theo đề, ta có; pi*x*căn x^2+25=pi*x*25
=>căn x^2+25=25
=>x^2+25=625
=>x^2=600
=>x=10*căn 6(cm)

Lời giải:
Diện tích xung quanh hình nón:
$\pi (r+R).l=\pi (6+3).4=36\pi$ (cm vuông)
Diện tích toàn phần:
$36\pi+\pi r^2+\pi R^2=36\pi +\pi.3^2+\pi. 6^2=81\pi$ (cm vuông)
Thể tích:
Chiều cao hình nón: $\sqrt{4^2-(6-3)^2}=\sqrt{7}$ (cm)
$\frac{1}{3}\pi (r^2+R^2+r.R)h=\frac{1}{3}\pi (3^2+6^2+3.6).\sqrt{7}=21\sqrt{7}\pi$ (cm khối)
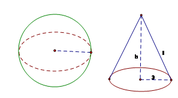
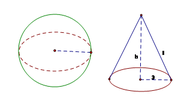

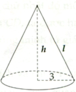



v nón =1/3 v trụ =1/3 pi r2 h=1/3 pi 32 4=12pi