
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đây là thấu kính hội tụ.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\Rightarrow d'=4,8cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{8}{4,8}\Rightarrow h'=0,6cm\)

Sử dụng công thức thấu kính phân kì:
1 f = 1 d ' - 1 d
Ta có: d ' = f d f + d = 12 . 8 12 + 8 = 4 , 8 c m
Đáp án: A

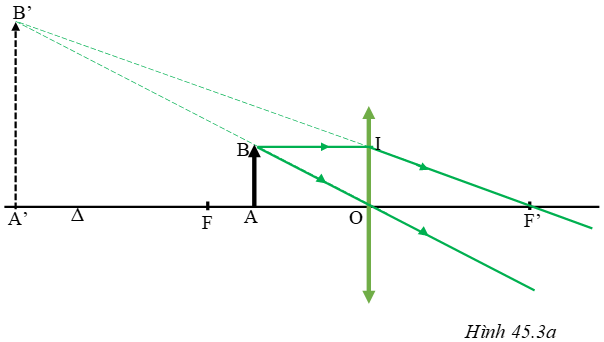
Đặt vật AB trong khoảng tiêu cự.
+ Ảnh của vật AB tạo bởi thấu kính hội tụ lớn hơn vật (H.45.3a).
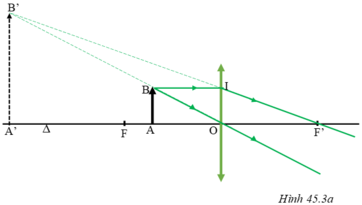
+ Ảnh của vật AB tạo bởi thấu kính phân kì nhỏ hơn vật (H.45.3).
![]()

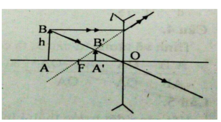
a) Xem hình 13G.
b) Sử dụng tam giác đồng dạng:
∆OA’B’ ~ ∆OAB
∆FB’O ~ ∆IB’B;
Ta tính được: h’ = 3,33cm; d’ = 8cm.

C5:
Đặt vật AB trong khoảng tiêu cự.
+ Ảnh của vật AB tạo bởi thấu kính hội tụ lớn hơn vật (H.45.2).
+ Ảnh của vật AB tạo bởi thấu kính phân kì nhỏ hơn vật (H.45.3)
C7:
- Xét 2 cặp tam giác đồng dạng trong hình 45.2: OB'F' và BB'I; OAB và OA'B'
Từ hệ thức đồng dạng, ta tính được h' = 3h = l,8cm; OA' = 24cm.
- Xét hai cặp tam giác đồng dạng trong hình 45.3: FB'O và IB'B; OA'B' và OAB.
Từ hệ thức đồng dạng, ta tính được: h' = 0,36cm; OA' = 4,8cm.
+ Ảnh của vật AB tạo bởi thấu kính phân kì nhỏ hơn vật (H.45.3).
C5.
+ Thấu kính là hội tụ: Ảnh của vật AB (hình 45.4) tạo bởi thấu kính hội tụ lớn hơn vật.
+ Thấu kính là phân kì: Ảnh của vật AB(hình 45.5) tạo bởi thấu kính phân kì nhỏ hơn vật.
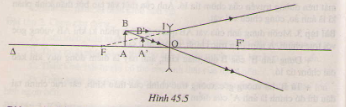
C7.
Tam giác BB'I đồng dạng với tam giác OB'F' cho ta:
BIOF=BB′OB′BIOF=BB′OB′ => 812=BB′OB′812=BB′OB′ => 128=OB′BB′128=OB′BB′ => BB′+OBBB′BB′+OBBB′ = 1,5
1 + OBBB′OBBB′ = 1,5 => OBBB′OBBB′ = 0,5 = 1212 => BB′OBBB′OB = 2
Tam giác OAB đồng dạng với tam giác OA'B', cho ta:
OA′OA=A′B′AB=OB′OBOA′OA=A′B′AB=OB′OB (*)
Ta tính tỉ số: OB′OBOB′OB = OB+BB′O

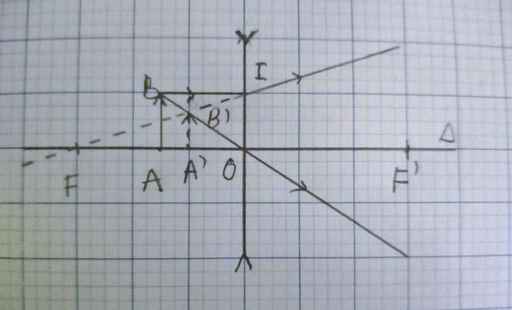
Tham khảo hình vẽ!!!
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow\dfrac{4}{A'B'}=\dfrac{4}{OA'}\left(1\right)\)
\(\Delta FA'B'\sim\Delta FOI\)
\(\Rightarrow\dfrac{OI}{A'B'}=\dfrac{OF}{OF-OA'}=\dfrac{OA}{A'B'}\)
\(\Rightarrow\dfrac{4}{A'B'}=\dfrac{12}{12-OA'}\left(2\right)\)
\(\Rightarrow\dfrac{4}{OA'}=\dfrac{12}{12-OA'}\Rightarrow OA'=3cm\)
\(\Rightarrow A'B'=\dfrac{AB\cdot OA'}{OA}=\dfrac{4\cdot3}{4}=3cm\)

F F' A B A' B' O
ảnh A'B' là ảnh thật, cùng chiều và lớn hơn vật
xétΔOAB và ΔOA'B'
\(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\)⇒\(\dfrac{AB}{A'B'}=\dfrac{8}{OA'}\left(1\right)\)
xétΔOFI và ΔF'A'B'
\(\dfrac{OI}{A'B'}=\dfrac{12}{OF'+OA'}\)(2)
từ (1) và (2)⇒\(\dfrac{8}{OA'}=\dfrac{12}{12+OA'}\)
⇔8.(12+OA')=12.OA'
⇔96+8.OA'=12.OA'
⇔8.OA'-12.OA'=96
⇔-4.OA'=96
⇔OA'=-24 cm
thay OA'=-24 vào (1)
\(\dfrac{1}{A'B'}=\dfrac{8}{-24}\)⇒A'B'=\(-\dfrac{1}{3}\) cm
Vị trí đặt ảnh:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\Rightarrow d'=4,8cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{8}{4,8}\Rightarrow h'=0,6cm\)