Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B x x x x 20 cm
Mình vẽ hơi xấu nên nó k bằng nhau ^_^
a) ta thấy chiều dài của hcn B là cạnh của đáy S
Cạnh đầu tiên của đáy là 20 - 2x
Ta thấy chiều dài của hcn A là cạnh của đáy S
Cạnh thứ hai của đáy là 20 - 2x
Vậy Diện tích đáy S là (20 - 2x)2
b) khi gấp lại thành hình hộp chữ nhật thì x cũng là chiều cao của hình nên
Thể tích HHCN là x(20 - 2x)2

Kim tự tháp có dạng hình chóp tứ giác đều S.ABCD.
Gọi M là trung điểm của cạnh CD; O là tâm của đáy ABCD.
Tính được:
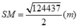
Diện tích xung quanh của kim tự tháp là:
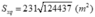
Thể tích của kim tự tháp:
V = 2436819 (m3)
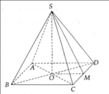
Để tính cạnh bên và diện tích một mặt bên của kim tự tháp Kê-ốp, chúng ta cần sử dụng các tính chất của hình chóp tứ giác đều.
1. **Tính cạnh bên**:
Trong một hình chóp tứ giác đều, cạnh bên có thể tính được bằng cách sử dụng định lý Pythagoras trên một tam giác vuông có cạnh góc vuông là nửa đường chéo của đáy (đường chéo chia đáy thành hai phần bằng nhau), độ dài một cạnh của đáy và chiều cao của hình chóp.
Trong trường hợp này, nửa đường chéo của đáy là \( \frac{231}{2} = 115.5 \) m, chiều cao của hình chóp là 137 m. Ta sẽ tính độ dài cạnh bên như sau:
\[ \text{Cạnh bên} = \sqrt{{\text{đường chéo}^2 + \text{chiều cao}^2}} \]
\[ \text{Cạnh bên} = \sqrt{{115.5^2 + 137^2}} \]
\[ \text{Cạnh bên} ≈ \sqrt{{13340.25 + 18769}} \]
\[ \text{Cạnh bên} ≈ \sqrt{{32109.25}} \]
\[ \text{Cạnh bên} ≈ 179.25 \, \text{m} \]
2. **Tính diện tích một mặt bên**:
Diện tích một mặt bên của hình chóp tứ giác đều được tính bằng công thức:
\[ \text{Diện tích một mặt bên} = \frac{{\text{cạnh đáy} \times \text{chiều cao}}}{{2}} \]
Trong trường hợp này, cạnh đáy là 231 m và chiều cao là 137 m. Ta sẽ tính diện tích một mặt bên như sau:
\[ \text{Diện tích một mặt bên} = \frac{{231 \times 137}}{{2}} \]
\[ \text{Diện tích một mặt bên} = \frac{{31647}}{{2}} \]
\[ \text{Diện tích một mặt bên} = 15823.5 \, \text{m}^2 \]
Vậy, cạnh bên của kim tự tháp Kê-ốp là khoảng 179.25 m và diện tích của một mặt bên là khoảng 15823.5 \( \text{m}^2 \).


Bài giảng học thử
Video không hỗ trỡ trên thiết bị của bạn!
Bài 9: Hình chữ nhật - Phần 1 - Toán 8 - Cô Diệu Linh
Video không hỗ trỡ trên thiết bị của bạn!
Bài 1. Định lí Ta-lét trong tam giác - Phần 1 - Toán 8 - Thầy Phan Toàn
Video không hỗ trỡ trên thiết bị của bạn!
Bài 4. Đường trung bình của tam giác, của hình thang - Phần 2 - Toán 8 - Thầy Phan Toàn
Video không hỗ trỡ trên thiết bị của bạn!
Bài 3. Hình thang cân - Phần 3 - Toán 8 - Thầy Phan Toàn
Video không hỗ trỡ trên thiết bị của bạn!
Bài 4. Khái niệm hai tam giác đồng dạng - Phần 2 - Toán 8 - Thầy Phan Toàn

Thể tích lượng nước còn lại trong hộp bằng hiệu giữa thể tích của hình hộp chữ nhật và thể tích của hình chóp đều. Vậy thể tích lượng còn lại là: 290 (cm3).


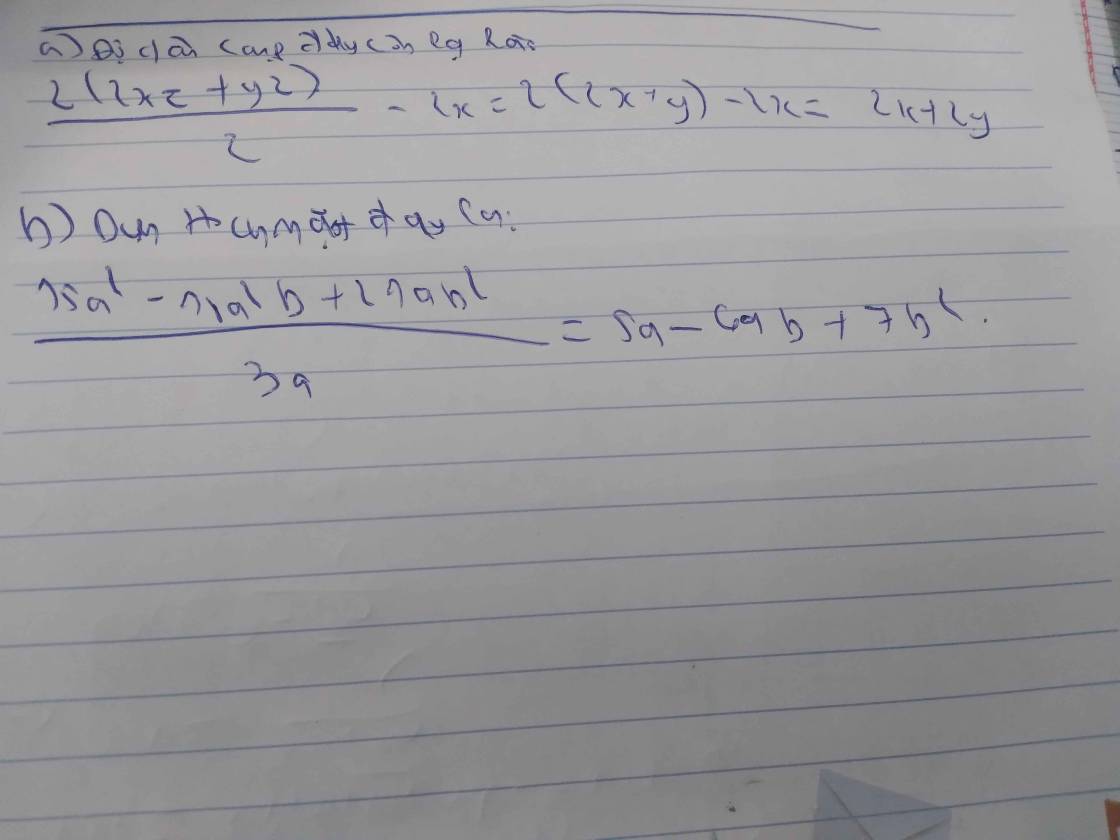
a) Chiều cao phần trên tháp:
\(19,2-12=7,2\left(m\right)\)
b) Thể tích hình hộp chữ nhật là:
\(V=S.h=\left(5\cdot5\right)\cdot12=300\left(m^3\right)\)
Thể tích hình chóp là:
\(V=\dfrac{1}{3}Sh=\dfrac{1}{3}\left(5\cdot5\right)\cdot7,2=60\left(m^3\right)\)
Thể tích tháp đồng hồ là:
\(300+60=360\left(m^3\right)\)
a) Chiều cao của phần trên của tháp đồng hồ:
19,2 - 12 = 7,2 (m)
b) Thể tích đáy:
5 . 5 . 12 = 300 (m³)
Thể tích phần trên của tháp:
5 . 5 . 7,2 : 3 = 60 (m³)
Thể tích của tháp đồng hồ:
300 + 60 = 360 (m³)