K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 8 2020
a) Ta có: \(x^5+x-1\)
\(=x^5-x^4+x^3+x^4-x^3+x^2-x^2+x-1\)
\(=x^3\left(x^2-x+1\right)+x^2\left(x^2-x+1\right)-\left(x^2-x+1\right)\)
\(=\left(x^2-x+1\right)\left(x^3+x^2-1\right)\)
b) Ta có: \(x^5+x^4+1\)
\(=x^5+x^4+x^3-x^3+1\)
\(=x^3\left(x^2+x+1\right)-\left(x^3-1\right)\)
\(=x^3\left(x^2+x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\)
\(=\left(x^3+x+1\right)\left(x^3-x+1\right)\)
c) Ta có: \(x^7+x^2+1\)
\(=x^7+x^6+x^5-x^6-x^5-x^4+x^4+x^3+x^2-x^3-x^2-x+x^2+x+1\)
\(=x^5\left(x^2+x+1\right)-x^4\left(x^2+x+1\right)+x^2\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)
d) Ta có: \(x^7+x^5+1\)
\(=x^7+x^6+x^5-x^6+1\)
\(=x^5\left(x^2+x+1\right)-\left(x^6-1\right)\)
\(=x^5\left(x^2+x+1\right)-\left(x^3+1\right)\left(x^3-1\right)\)
\(=x^5\left(x^2+x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\left(x^3+1\right)\)
\(=\left(x^2+x+1\right)\left[x^5-\left(x-1\right)\left(x^3+1\right)\right]\)
\(=\left(x^2+x+1\right)\left[x^5-\left(x^4+x-x^3-1\right)\right]\)
\(=\left(x^2+x+1\right)\left(x^5-x^4-x+x^3+1\right)\)
e) Ta có: \(x^8+x^7+1\)
\(=x^8+x^7+x^6-\left(x^6-1\right)\)
\(=x^6\left(x^2+x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\left(x^3+1\right)\)
\(=\left(x^2+x+1\right)\left[x^6-\left(x-1\right)\left(x^3+1\right)\right]\)
\(=\left(x^2+x+1\right)\left[x^6-\left(x^4+x-x^3-1\right)\right]\)
\(=\left(x^2+x+1\right)\left(x^6-x^4-x+x^3+1\right)\)
f) Ta có: \(x^{10}+x^5+1\)
\(=\left(x^{10}-x\right)+\left(x^5-x^2\right)+\left(x^2+x+1\right)\)
\(=x\left(x^9-1\right)+x^2\left(x-1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x^2+x+1\right)\left(x^6+x^3+1\right)+x^2\left(x-1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left[\left(x^2-x\right)\left(x^6+x^3+1\right)+x^3-x^2+1\right]\)
\(=\left(x^2+x+1\right)\left[x^8+x^5+x^2-x^7-x^4-x+x^3-x^2+1\right]\)
\(=\left(x^2+x+1\right)\left(x^8-x^7+x^5-x^4+x^3-x+1\right)\)
NM
1
PN
0
VT
2
17 tháng 6 2017
Ta có:
(x + y)3 = x3 + y3 + 3xy(x + y) = 1
=> a + 3xy = 1 => a = 1 - 3xy
5a(a + 1) = 5(1 - 3xy)(2 - 3xy) = 5(2 - 9xy + 9x2y2)
= 10 - 45xy + 45x2y2 (1)
(x + y)5 = x5 + y5 + 5xy(x3 + x2y + x2y + xy2 + xy2 + y3) = 1
=> b + 5xy(x + y)(x2 + xy + y2) = 1
=> b + 5xy(x2 + xy + y2) = 1 (
=> b + 5xy(x + y)2 - 5x2y2 = 1
=> b = 1 + 5x2y2 - 5xy
=> 9b + 1 = 9 + 45x2y2 - 45xy + 1 = 10 + 45x2y2 - 45xy (2)
Từ (1) và (2) => 5a(a + 1) = 1 + 9b (đpcm)
NR
1
AT
26 tháng 6 2018
a/ \(\left(x^2-2x+2\right)\left(x^2-2x+5\right)=40\)
Đặt: \(x^2-2x+1=t\left(t\ge0\right)\)
\(pt\Leftrightarrow\left(t+1\right)\left(t+4\right)=40\)
\(\Leftrightarrow t^2+5t-36=0\)
\(\Leftrightarrow t^2-4t+9t-36=0\)
\(\Leftrightarrow t\left(t-4\right)+9\left(t-4\right)=0\)
\(\Leftrightarrow\left(t-4\right)\left(t+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t-4=0\\t+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=4\left(tm\right)\\t=-9\left(ktm\right)\end{matrix}\right.\)
Ta có: t = 4 => \(x^2-2x+1=4\)
\(\Leftrightarrow\left(x-1\right)^2=4\Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Vậy..............
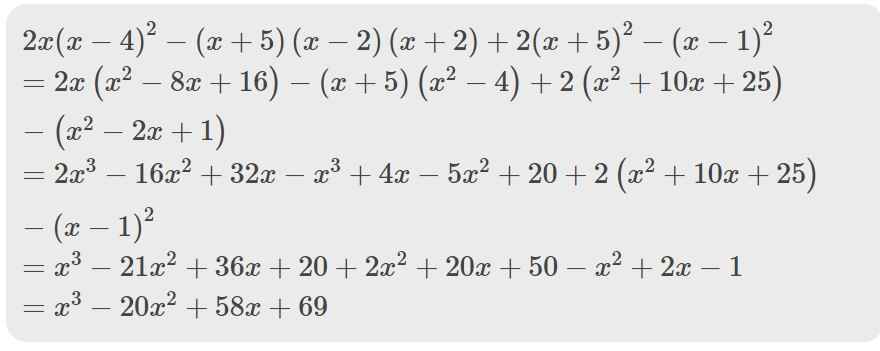
x5+x+1=(x5+x4+x3)-(x4+x3+x2)+(x2+x+1)=x3(x2+x+1)-x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x3-x2+1)
mình chỉ mới lớp 7 hông giải được
sorry nha