VA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
RG
5 tháng 12 2018
1/ \(\frac{x-3}{3xy}\)+\(\frac{5x+3}{3xy}\)= \(\frac{6x}{3xy}\)=\(\frac{3}{y}\)
2/\(\frac{5x-7}{2x-3}\)+\(\frac{4-3x}{2x-3}\)=\(\frac{2x-3}{2x-3}\)=1
3/\(\frac{11x-7}{3-5x}\)-\(\frac{6x+4}{5x-3}\)=\(\frac{11x-7}{3-5x}\)+\(\frac{6x+4}{3-5x}\)=\(\frac{17x-3}{3-5x}\)
4/\(\frac{3}{2x+6}\)-\(\frac{x-6}{2x^2+6x}\)=\(\frac{3x}{x\left(2x+6\right)}\)-\(\frac{x-6}{x\left(2x+6\right)}\)=\(\frac{2x-6}{x\left(2x+6\right)}\)
5/\(\frac{1}{2x-10}\)+\(\frac{2x}{3x^2-15x}\)=\(\frac{1}{2\left(x-5\right)}\)+\(\frac{2x}{3x\left(x-5\right)}\)=\(\frac{3x}{6x \left(x-5\right)}\)+\(\frac{4x}{6x\left(x-5\right)}\)
=\(\frac{7x}{6x\left(x-5\right)}\)=\(\frac{7}{6\left(x-5\right)}\)
16 tháng 2 2017
b,(2x -3 )(3x - 1) =(2x+3)(x-2)
<=> 6x2 - 11x + 3 = 2x2 - x - 6
<=.> 4x2 - 10x + 9 = 0
<=> (2x - \(\frac{5}{2}\))2 +\(\frac{11}{4}\)= 0 ( vô lí )
( Vì (2x - \(\frac{5}{2}\))2 \(\ge\) 0 => (2x - \(\frac{5}{2}\))2 + \(\frac{11}{4}\)\(\ge\)\(\frac{11}{4}\))
Vậy pt vô nghiệm
CP
17 tháng 2 2017
câu C : (4-3x)(2x+3)=(5-2x)(3x-4)
<=> (4-3x)(2x+3)-(5-2x)(4-3x)=0
<=>(4-3x)(2x+3-5+2x)=0
<=>(4-3x)(4x-2)=0
<=>\(\left[\begin{matrix}3x=4\\4x=2\end{matrix}\right.\)
<=>\(\left[\begin{matrix}x=\frac{4}{3}\\x=\frac{1}{2}\end{matrix}\right.\)
4 tháng 3 2021
a) \(4x^4+4x^3+5x^2+2x+1\)
= \(x^2\left(4x^2+4x+5+\frac{4}{x}+\frac{1}{x^2}\right)\)
=\(x^2\left[\left(4x^2+\frac{1}{x^2}\right)+2\left(2x+\frac{1}{x}\right)+5\right]\)(1)
Đặt \(2x+\frac{1}{x}=a\)thì \(\left(2x+\frac{1}{x}\right)^2=a^2\)\(\Rightarrow4x^2+\frac{1}{x^2}=a^2-4\)
Thay vào (1), ta có:
\(x^2\left(a^2-4+2a+5\right)\)
=\(x^2\left(a^2+2a+1\right)\)
=\(x^2\left(a+1\right)^2\)
=\(\left[x\left(a+1\right)\right]^2\)
=\(\left[x\left(2x+\frac{1}{x}+1\right)\right]^2\)
=\(\left(2x^2+1+x\right)^2\)
\(=\left(2x^2+x+1\right)^2\)
3 tháng 3 2021
a) Đặt f(x) = 4x4 + 4x3 + 5x2 + 2x + 1
Sau khi phân tích thì đa thức có dạng ( 2x2 + ax + 1 )( 2x2 + bx + 1 )
=> f(x) = ( 2x2 + ax + 1 )( 2x2 + bx + 1 )
<=> f(x) = 4x4 + 2bx3 + 2x2 + 2ax3 + abx2 + ax + 2x2 + bx + 1
<=> f(x) = 4x4 + ( a + b )2x3 + ( ab + 4 )x2 + ( a + b )x + 1
Đồng nhất hệ số ta có : \(\hept{\begin{cases}a+b=2\\ab=1\end{cases}\Leftrightarrow}a=b=1\)
Vậy f(x) = 4x4 + 4x3 + 5x2 + 2x + 1 = ( 2x2 + x + 1 )2
b) 3x4 + 11x3 - 7x2 - 2x + 1
= 3x4 - x3 + 12x3 - 4x2 - 3x2 + x - 3x + 1
= x3( 3x - 1 ) + 4x2( 3x - 1 ) - x( 3x - 1 ) - ( 3x - 1 )
= ( 3x - 1 )( x3 + 4x2 - x - 1 )
GF
1
NN
29 tháng 11 2017
a) \(\dfrac{4x-1}{3x^2y}-\dfrac{7x-1}{3x^2y}\)
\(=\dfrac{\left(4x-1\right)-\left(7x-1\right)}{3x^2y}\)
\(=\dfrac{4x-1-7x+1}{3x^2y}\)
\(=\dfrac{-3x}{3x^2y}\)
\(=\dfrac{-1}{xy}\)
b) \(\dfrac{4x+5}{2x-1}-\dfrac{5-9x}{2x-1}\)
\(=\dfrac{\left(4x+5\right)-\left(5-9x\right)}{2x-1}\)
\(=\dfrac{4x+5-5+9x}{2x-1}\)
\(=\dfrac{13x}{2x-1}\)
c) \(\dfrac{11x}{2x-3}-\dfrac{x-18}{3-2x}\)
\(=\dfrac{11x}{2x-3}+\dfrac{x-18}{2x-3}\)
\(=\dfrac{11x+\left(x-18\right)}{2x-3}\)
\(=\dfrac{11x+x-18}{2x-3}\)
\(=\dfrac{12x-18}{2x-3}\)
\(=\dfrac{6\left(2x-3\right)}{2x-3}\)
\(=\dfrac{6}{1}\)
\(=6\)
d) \(\dfrac{2x-7}{10x-4}-\dfrac{3x+5}{4-10x}\)
\(=\dfrac{2x-7}{10x-4}+\dfrac{3x+5}{10x-4}\)
\(=\dfrac{\left(2x-7\right)+\left(3x+5\right)}{10x-4}\)
\(=\dfrac{2x-7+3x+5}{10x-4}\)
\(=\dfrac{5x-2}{10x-4}\)
\(=\dfrac{5x-2}{2\left(5x-2\right)}\)
\(=\dfrac{1}{2}\)
20 tháng 2 2017
\(A=\frac{1-x}{x+1}+3=\frac{2x+3}{x+1}\Leftrightarrow\frac{1-x+3x+3-2x-3}{x+1}=\frac{1}{x+1}=0\)
Vô nghiệm.
\(B=\left(5,5-11x\right)\left(\frac{7x+2}{5}+\frac{2\left(1-3x\right)}{3}\right)=0\)
\(\left[\begin{matrix}5,5-11x=0\\3\left(7x+2\right)+10-30x=0\end{matrix}\right.\Leftrightarrow\left[\begin{matrix}x=\frac{5,5}{11}\\-9x+16=0\end{matrix}\right.\)\(\left[\begin{matrix}x=\frac{1}{2}\\x=\frac{16}{9}\end{matrix}\right.\)
20 tháng 2 2017
b) (5,5-11x)(\(\frac{7x+2}{5}\)+ \(\frac{2\left(1-3x\right)}{3}\)) = 0
<=> (5,5 - 11x )(\(\frac{-9x+16}{15}\))=0
<=>\(\left[\begin{matrix}5,5-11x=0\\\frac{-9x+16}{15}=0\end{matrix}\right.\)
<=> \(\left[\begin{matrix}x=\frac{1}{2}\\x=\frac{16}{9}\end{matrix}\right.\)
Vậy pt có nghiệm là x=\(\frac{1}{2}\) và x= \(\frac{16}{9}\)
10 tháng 8 2017
a) \(\dfrac{2x+3}{x-5}=\dfrac{2\left(x-5\right)+13}{x-5}=2+\dfrac{13}{x-5}\)
Để \(2+\dfrac{13}{x-5}\in Z\)
thì \(\dfrac{13}{x-5}\in Z\Rightarrow13⋮x-5\)
\(\Rightarrow x-5\inƯ\left(13\right)\)
\(\Rightarrow x-5\in\left\{\pm1;\pm13\right\}\)
Xét các trường hợp...
b) \(\dfrac{x^3-x^2+2}{x-1}=\dfrac{x^2\left(x-1\right)+2}{x-1}=x^2+\dfrac{2}{x-1}\)
Tương tự câu a)
c) \(\dfrac{x^3-2x^2+4}{x-2}=\dfrac{x^2\left(x-2\right)+4}{x-2}=x^2+\dfrac{4}{x-2}\)
...
d) \(\dfrac{2x^3+x^2+2x+2}{2x+1}=\dfrac{x^2\left(2x+1\right)+2x+2}{2x+1}=x^2+\dfrac{2x+2}{2x+1}\)
Khi đó lí luận cho \(2x+2⋮2x+1\)
\(\Rightarrow\left(2x+1\right)+1⋮2x+1\)
\(\Rightarrow1⋮2x+1\)
\(\Rightarrow2x+1\inƯ\left(1\right)\)
...
e) \(\dfrac{3x^3-7x^2+11x-1}{3x-1}=\dfrac{x^2\left(3x-1\right)-2x\left(3x-1\right)+3\left(3x-1\right)+2}{3x-1}\)
\(=\dfrac{\left(x^2-2x+3\right)\left(3x-1\right)+2}{3x-1}=\left(x^2-2x+3\right)+\dfrac{2}{3x-1}\)
...
f) \(\dfrac{x^4-16}{x^4-4x^3+8x^2-16x+16}=\dfrac{\left(x^2\right)^2-4^2}{\left(x-2\right)^2\left(x^2+4\right)}\)
\(=\dfrac{\left(x^2-4\right)\left(x^2+4\right)}{\left(x-2\right)^2\left(x^2+4\right)}=\dfrac{x^2-4}{\left(x-2\right)^2}=\dfrac{x+2}{x-2}=\dfrac{\left(x-2\right)+4}{x-2}=1+\dfrac{4}{x-2}\)
....
15 tháng 4 2018
Giải các phương trình
\(a,3x-2=2x-3\)
\(\Leftrightarrow3x-2x=-3+2\)
\(\Leftrightarrow x=-1\)
Vậy pt có tập nghiệm S = { - 1 }
\(b,2x+3=5x+9\)
\(\Leftrightarrow2x-5x=9-3\)
\(\Leftrightarrow-3x=6\)
\(\Leftrightarrow x=-2\)
Vậy pt có tập nghiệm S = { - 2 }
\(c,11x+42-2x=100-9x-22\)
\(\Leftrightarrow11x-2x+9x=100-22-42\)
\(\Leftrightarrow18x=36\)
\(\Leftrightarrow x=2\)
Vậy pt có tập nghiệm S = { - 2 }
\(d,2x-\left(3-5x\right)=4\left(x+3\right)\)
\(\Leftrightarrow2x-3+5x=4x+12\)
\(\Leftrightarrow2x+5x-4x=12+3\)
\(\Leftrightarrow3x=15\)
\(\Leftrightarrow x=5\)
Vậy pt có tập nghiệm S = { - 5 }
\(e,\dfrac{3x+2}{2}-\dfrac{3x+1}{6}=\dfrac{5}{3}+2x\)
\(\Leftrightarrow\dfrac{3\left(3x+2\right)}{6}-\dfrac{3x+1}{6}=\dfrac{5.2}{6}+\dfrac{2x.6}{6}\)
\(\Leftrightarrow9x+6-3x-1=10+12x\)
\(\Leftrightarrow9x-3x-12x=10-6+1\)
\(\Leftrightarrow-6x=5\)
\(\Leftrightarrow x=-\dfrac{5}{6}\)
Vậy pt có tập nghiệm S = { - \(\dfrac{5}{6}\) }
f,\(\dfrac{x+4}{5}-x+4=\dfrac{x}{3}-\dfrac{x-2}{2}\)
\(\Leftrightarrow\dfrac{6\left(x+4\right)}{30}-\dfrac{30x}{30}+\dfrac{4.30}{30}=\dfrac{10x}{30}-\dfrac{15\left(x-2\right)}{30}\)
\(\Leftrightarrow6x+24-30x+120=10x-15x+30\)
\(\Leftrightarrow6x-30x-10x+15x=30-24-120\)
\(\Leftrightarrow-19x=-114\)
\(\Leftrightarrow x=6\)
Vậy pt có tập nghiệm S = { - 6 }
\(g,\left(2x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(1;-\dfrac{1}{2}\) }
\(h,\left(x+\dfrac{2}{3}\right)\left(x-\dfrac{1}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{2}{3}=0\\x-\dfrac{1}{2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(-\dfrac{2}{3};\dfrac{1}{2}\) }
\(i,\left(3x-1\right)\left(2x-3\right)\left(2x-3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(2x-3\right)^2\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\2x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{3}{2}\\x=-5\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(\dfrac{1}{3};\dfrac{3}{2};-5\) }
\(k,3x-15=2x\left(x-5\right)\)
\(\Leftrightarrow3x-15=2x^2-10x\)
\(\Leftrightarrow-2x^2+3x+10x=15\)
\(\Leftrightarrow-2x^2+13x-15=0\)
\(\Leftrightarrow-2x^2+10x+3x-15=0\)
\(\Leftrightarrow\left(x-5\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\3-2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(5;\dfrac{3}{2}\) }
\(m,\left|x-2\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { -1; 5 }
\(n,\left|x+1\right|=\left|2x+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=2x+3\\x+1=-2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { \(-2;-\dfrac{4}{3}\) }
\(j,\dfrac{7x-3}{x-1}=\dfrac{2}{3}\) ĐKXĐ : x≠ 1
\(\Leftrightarrow3\left(7x-3\right)=2\left(x-1\right)\)
\(\Leftrightarrow21x-9=2x-2\)
\(\Leftrightarrow x=\dfrac{7}{19}\) ( t/m )
Vậy pt có tập nghiệm S = { \(\dfrac{7}{19}\) }
đ, ĐKXĐ : x ≠ - 1
\(\dfrac{2\left(3-7x\right)}{1+x}=\dfrac{1}{2}\)
\(\Leftrightarrow4\left(3-7x\right)=1+x\)
\(\Leftrightarrow12-28x=1+x\)
\(\Leftrightarrow-29x=-11\)
\(\Leftrightarrow x=\dfrac{11}{29}\) ( t/m)
Vậy pt có tập nghiệm S = { \(\dfrac{11}{29}\) }
\(y,\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{20}{x^2-25}\) ĐKXĐ : \(\left\{{}\begin{matrix}x\ne5\\x\ne-5\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{\left(x+5\right)^2-\left(x-5\right)^2}{\left(x-5\right)\left(x+5\right)}=\dfrac{20}{\left(x-5\right)\left(x+5\right)}\)
\(\Rightarrow20x=20\)
\(\Leftrightarrow x=1\) ( t/m )
Vậy pt có tập nghiệm S = { 1 }
\(\dfrac{1}{x-1}+\dfrac{2}{x+1}=\dfrac{x}{x^2-1}\) ĐKXĐ : \(\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{x+1+2\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow3x-1=x\)
\(\Leftrightarrow2x=1\Leftrightarrow x=\dfrac{1}{2}\)( t/m)
Vậy pt có tập nghiệm S = { \(\dfrac{1}{2}\) }
S
28 tháng 6 2020
a) \(\left(x^2+x\right)^2-2\left(x^2+x\right)-15\)
Đặt \(x^2+x=t\), đa thức trở thành : \(t^2-2t-15\)
= \(\left(t+3\right)\left(t-5\right)\)
\(=\left(x^2+x+3\right)\left(x^2+x-5\right)\)
b) \(\left(a+b+c\right)^3-a^3-b^3-c^3\)
\(=a^3+b^3+c^3+2ab+2ac+2bc-a^3-b^3-c^3\)
\(=2ab+2ac+2bc=2\left(ab+ac+bc\right)\)
c) \(x-1+x^{n+3}-x^n\)
\(=x-1+x^n\left(x^3-1\right)\)
\(=x-1+x^n\left(x-1\right)\left(x^2+x+1\right)\)
\(=\left(x-1\right)\left(x^{n+2}+x^{n+1}+x^n+1\right)\)
d) \(2x^4-7x^3-2x^2+13x+6\)
\(=\left(2x^4+2x^3\right)-\left(9x^3+9x^2\right)+\left(7x^2+7x\right)+\left(6x+6\right)\)
\(=\left(x+1\right)\left(2x^3-9x^2+7x+6\right)\)
\(=\left(x+1\right)\left[\left(2x^3+x^2\right)-\left(10x^2+5x\right)+\left(12x+6\right)\right]\)
\(=\left(x+1\right)\left(2x+1\right)\left(x^2-5x+6\right)\)
\(=\left(x+1\right)\left(2x+1\right)\left(x-2\right)\left(x-3\right)\)
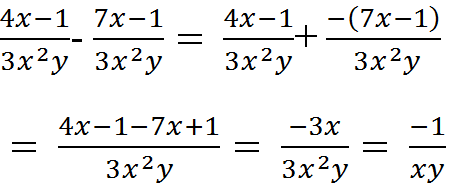
=3x4-x3+12x3-4x2-3x2+x-3x+1
=(3x4-x3)+(12x3-4x2)-(3x2-x)-(3x-1)
=x3(3x-1) + 4x2(3x-1) -x(3x-1) -(3x-1)
=(3x-1)(x3+4x2-x-1)