Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{x+9}{x^2-9}\)-\(\dfrac{3}{x^2+3x}\) = \(\dfrac{x+9}{\left(x-3\right)\left(x+3\right)}\)-\(\dfrac{3}{x\left(x+3\right)}\)
= \(\dfrac{x^2+9x-3x+9}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{x^2+6x+9}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{x+3}{x\left(x-3\right)}\)

Câu 5:
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật

a) \(\left(x+3\right)^3-x.\left(3x+1\right)^2+\left(2x+1\right).\left(4x^2-2x+1\right)-3x^2=54\)
\(\Leftrightarrow x^3+9x^2+27x+27-x.\left(9x^2+6x+1\right)+8x^3+1-3x^2=54\)
\(\Leftrightarrow x^3+9x^2+27x+27-9x^3-6x^2-x+8x^3+1-3x^2=54\)
\(\Leftrightarrow26x+28=54\Leftrightarrow26x=54-28\Leftrightarrow26x=26\Leftrightarrow x=1\)
Vậy nghiệm của phương trình là x=1
b) \(\left(x-3\right)^3-\left(x-3\right).\left(x^2+3x+9\right)+6.\left(x+1\right)^2+3x^2=-33\)
\(\Leftrightarrow x^3-9x^2+27x-27-\left(x^3-27\right)+6.\left(x^2+2x+1\right)+3x^2=-33\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+6x^2+12x+6+3x^2=-33\)
\(\Leftrightarrow27x+12x+6=-33\Leftrightarrow39x=-33-6\Leftrightarrow39x=-39\Leftrightarrow x=-1\)
Vậy nghiệm của phương trình là x = -1
Trần Anh: Hí hí =)) ÀI LỚP DIU CHIU CHIU CHÍU :3 CẢM ƠN PẠN NHIỀU NHÁ ;) ;) ;)

Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC

a: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
b: \(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
c: \(=\dfrac{6-7+x}{3\left(x-1\right)}=\dfrac{x-1}{3\left(x-1\right)}=\dfrac{1}{3}\)
d: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)

Ta có: \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=15\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+9\left(x^2+2x+1\right)=15\)
\(\Leftrightarrow-9x^2+27x+9x^2+18x+9=15\)
\(\Leftrightarrow45x=6\)
hay \(x=\dfrac{2}{15}\)

\(\dfrac{1}{x^2-4}+\dfrac{2x}{x+2}=\dfrac{1}{\left(x-2\right)\left(x+2\right)}+\dfrac{2x}{x+2}=\dfrac{1+2x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{1+2x^2-4x}{\left(x+2\right)\left(x-2\right)}\)
trên bài mink đã ẩn đi bước quy đồng!!
\(\dfrac{18}{\left(x-3\right)\left(x^2-9\right)}-\dfrac{3}{x^2-6x+9}-\dfrac{x}{x^2-9}=\dfrac{18}{\left(x-3\right)\left(x+3\right)\left(x-3\right)}-\dfrac{3}{\left(x-3\right)^2}-\dfrac{x}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{18}{\left(x-3\right)^2\left(x+3\right)}-\dfrac{3}{\left(x-3\right)^2}-\dfrac{x}{\left(x-3\right)\left(x+3\right)}=\dfrac{18-3\left(x+3\right)-x\left(x-3\right)}{\left(x-3\right)^2\left(x+3\right)}\)
\(=\dfrac{18-3x-9-x^2+3x}{\left(x-3\right)^2\left(x+3\right)}=\dfrac{9-x^2}{\left(x-3\right)^2\left(x+3\right)}=\dfrac{-\left(x-3\right)\left(x+3\right)}{\left(x-3\right)^2\left(x+3\right)}=\dfrac{-1}{x-3}\)
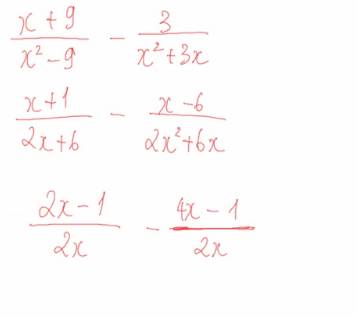
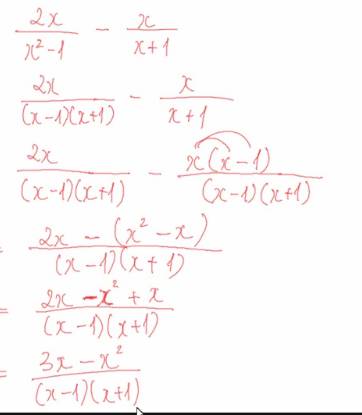





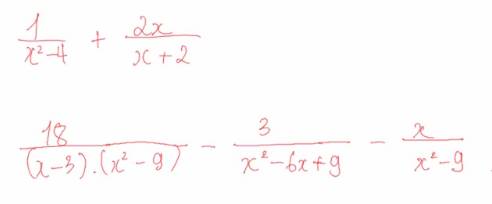
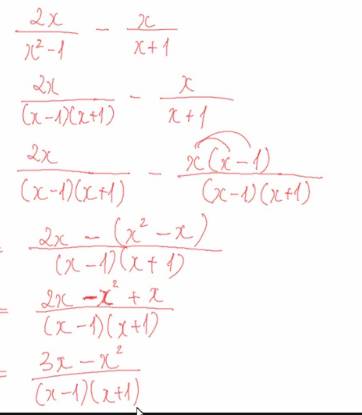
\(2x-1-x^2\\ =x+x-1-x^2\\ =\left(x-x^2\right)+\left(x-1\right)\\ =-x\left(x-1\right)+\left(x-1\right)\\ =\left(x-1\right)\left(1-x\right)\)
2x - 1 - x²
= -x² + 2x - 1
= -(x² - 2x + 1)
= -(x - 1)²