
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


P = |x – 2015| + |x – 2016| + |x – 2017|
P = (|x – 2015| + |2017 – x|) + |x – 2016|
Vì |x – 2015| + |2017 – x| \(\ge\) |x – 2015 + 2017 – x| = 2 với mọi x
=> (|x – 2015| + |2017 – x|) + |x – 2016| \(\ge\) 2 + |x – 2016| \(\ge\) 2 với mọi x
=> P \(\ge\) 2 với mọi x
Dấu “=” xảy ra ó x = 2016
Vậy minP = 2 tại x = 2016
Lâu chưa làm nên không chắc lắm


a/b=c/d =>a/c=b/d
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
\(\Rightarrow\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2\)\(\Leftrightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\left(\frac{a+b}{b+d}\right)^2=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\)
\(\Rightarrow dpcm\)

Câu 1: B
Câu 2: C
Câu 3: D
Câu 4: C
Câu 5: A
Câu 6: B
Câu 7: D
Câu 8: A
Câu 9: A
Câu 10: B


Chứng tỏ rằng đa thức Q(x) = x4 + 2015x2 + 2016 không có nghiệm.
Ta có x4 \(\ge\)0 \(\forall\)x
và 2015.x2 \(\ge\)0 \(\forall\)x
->x4 + 2015x2 + 2016 \(\ge\)0 \(\forall\)x
hay đa thức Q(X) ko có nghiệm.


1)\(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}\)
\(A< \dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{99.100}\)
\(A< \dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A< \dfrac{1}{4}-\dfrac{1}{100}\)
\(A< \dfrac{1}{4}\)(1)
\(A>\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{100.101}\)
\(A>\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{100}-\dfrac{1}{101}\)
\(A>\dfrac{1}{5}-\dfrac{1}{101}\)
\(A>\dfrac{96}{505}>\dfrac{1}{6}\)
\(A>\dfrac{1}{6}\)(2)
Từ (1) và (2)
\(\dfrac{1}{6}< A< \dfrac{1}{4}\)
2)
\(A=\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+...+\dfrac{1}{92.95}+\dfrac{1}{95.98}\)
\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{92}-\dfrac{1}{95}+\dfrac{1}{95}-\dfrac{1}{98}\right)\)\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{98}\right)\)
\(A=\dfrac{1}{3}.\dfrac{24}{49}=\dfrac{8}{49}\)
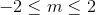 B.
B. 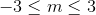
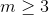

 xv,vfbv,f
xv,vfbv,f
 gcghgcgh
gcghgcgh




\(A.-2\le m\le2\)
\(B.-3\le m\le3\)
\(C.m\ge3\)
Đề bài đó nó lỗi nên biến mất nhé