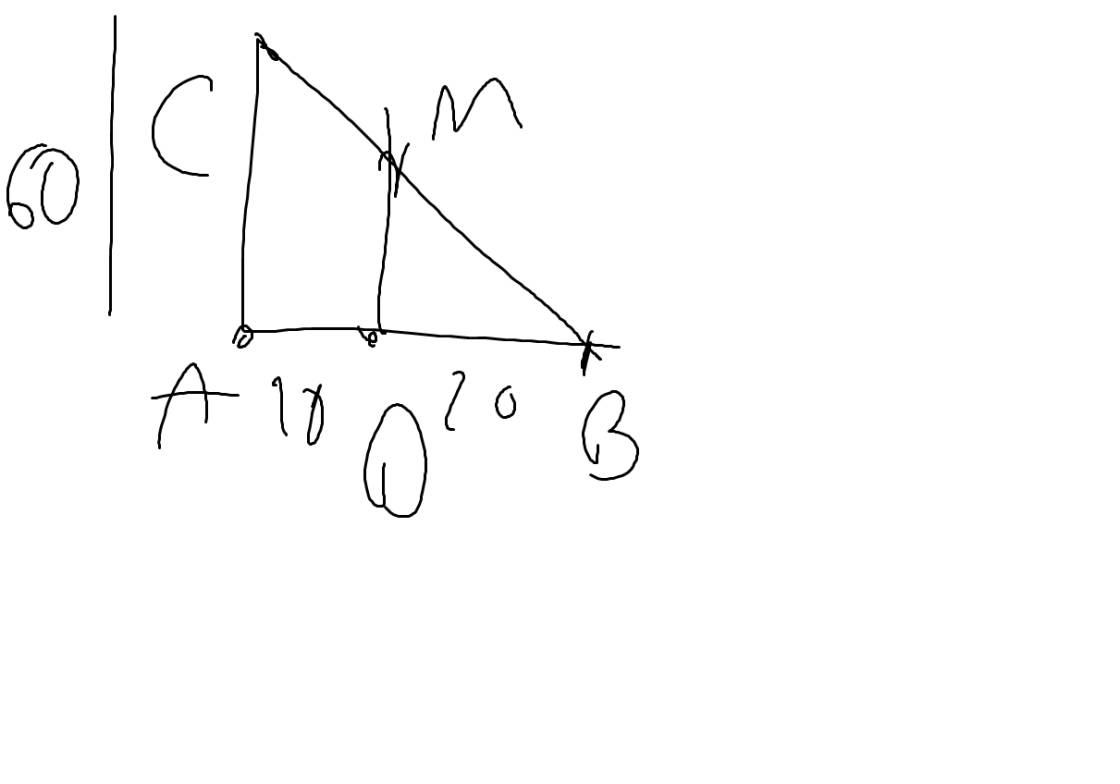Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi A là đáy, H là chiều cao
Theo đề bài ta có:
A
x
H
2
= 72 và
A
12
=
H
3
A
12
=
H
x
4
3
x
4
=
a) Gọi A là đáy, H là chiều cao
Theo đề bài ta có:
AxH2AxH2 = 72 và A12A12 = H3H3
A12A12 = Hx43x4Hx43x4 =

B A C
Tổng của cạnh AB và AC là:
24 - 10 = 14 ( cm )
Ta có sơ đồ:
Cạnh AB:|-------|-------|-------| } 14 cm
Cạnh AC:|-------|-------|-------|-------|
Cạnh AB là:
14 : 7 x 3 = 6 ( cm )
Cạnh AC là:
14 - 6 = 8 ( cm )
Diện tích ABC là:
\(\frac{8\times6}{2}=24\)( cm2)
Đáp số: 24 cm2
A B C
Tổng độ dài hai cạnh AB và AC là:
\(AB+AC=24-10=14\left(cm\right)\)
Độ dài cạnh AB là:
\(AB=14:\left(3+4\right).3=6\left(cm\right)\)
Độ dài cạnh AC là:
\(AC=14-6=8\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\frac{\left(AB.AC\right)}{2}=\frac{6.8}{2}=24\left(cm^2\right)\)

Tổng số đo cạnh AB và AC là :
24 - 10 = 14 ( cm )
Coi cạnh góc vuông AB gồm ba phần bằng nhau thì cạnh góc vuông AC gồm bốn phần.
B A C
độ dài cạnh AB là :
14 : ( 3 + 4 ) x 3 = 6 ( cm )
độ dài cạnh AC là :
14 - 6 = 8 ( cm )
Diện tích tam giác ABC là :
( 8 x 6 ) : 2 = 24 ( cm2 )
đáp số : 24 cm2

MDAC là hình thang có chiều cao 10cm
=>MD//AC và AD=10cm
DB+AD=AB
=>DB+10=30
=>DB=20(cm)
Xét ΔBAC có MD//AC
nên \(\dfrac{MD}{AC}=\dfrac{BD}{BA}\)
=>\(\dfrac{MD}{60}=\dfrac{20}{30}=\dfrac{2}{3}\)
=>\(MD=60\cdot\dfrac{2}{3}=40\left(cm\right)\)
Diện tích hình thang ADMC là:
\(S_{ADMC}=\dfrac{1}{2}\cdot AD\cdot\left(MD+AC\right)\)
\(=\dfrac{1}{2}\cdot10\cdot\left(60+40\right)=5\cdot100=500\left(cm^2\right)\)
Diện tích tam giác ABC là:
\(S_{ACB}=\dfrac{1}{2}\cdot AB\cdot AC=900\left(cm^2\right)\)
\(S_{ABC}=S_{BMD}+S_{CMDA}\)
=>\(S_{BMD}+500=900\)
=>\(S_{DMB}=400\left(cm^2\right)\)