Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)

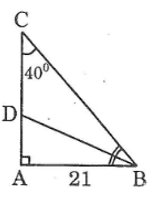
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

Bạn viết đề sai rồi
Cái \(3\dfrac{14}{17}\) là hỗn số chứ ko phải là số tự nhiên nhân vs phân số
#)Giải :
(Hình bn tự vẽ)
AD là phân giác của ∆ABC \(\Rightarrow\) \(\frac{BD}{AB}=\frac{DC}{AC}\Rightarrow\frac{BD^2}{AB^2}=\frac{DC^2}{AC^2}\)
Ta có : \(BC=BD+CD=3.\frac{14}{17}+9.\frac{3}{17}=\frac{42}{17}+\frac{27}{17}=\frac{69}{17}\)
Mà ∆ABC vuông tại A nên theo định lí Py - ta - go \(\Rightarrow AB^2+AC^2=BC^2\Rightarrow AB^2+AC^2=\left(\frac{69}{17}\right)^2\)
Theo t/chất dãy tỉ số bằng nhau : \(\frac{BD^2}{AB^2}=\frac{DC^2}{AC^2}=\frac{BD^2+DC^2}{AB^2+AC^2}=\frac{\left(\frac{42}{17}\right)^2+\left(\frac{27}{17}\right)^2}{\left(\frac{69}{17}\right)^2}=\) dài dòng vãi ra @@
Chắc đề sai rồi

a)Ta có: SinC = \(\frac{AB}{BC}\)=> Sin40 = \(\frac{10}{BC}\)=> BC = 15.5 (cm)
b) Có B = 90 độ - 40 độ = 60 độ
=> Góc ABD = 60/2 = 30 độ
Ta có TanABD = \(\frac{AD}{BA}\)=> Tan30 = \(\frac{AD}{10}\)=> AD = \(\frac{\sqrt{3}\cdot10}{3}\)

Trên tia đối của tia BA lấy I sao cho BI = DQ
\(\Delta DCQ=\Delta BCI\left(c.g.c\right)\Rightarrow\hept{\begin{cases}CQ=CI\\\widehat{DCQ}=\widehat{BCI}\end{cases}}\)
Ta có: \(\widehat{QCI}=\widehat{QCB}+\widehat{BCI}=\widehat{QCB}+\widehat{DCQ}=\widehat{BCD}=90^0\)
Ta có: \(AP+AQ+PQ=2AB\)
\(\Rightarrow AP+AQ+PQ=AP+PB+AQ+QD\)
\(\Rightarrow PQ=PB+QD\)
\(\Rightarrow PQ=PB+BI\Rightarrow PQ=PI\)
\(\Delta PCQ=\Delta PCI\left(c.c.c\right)\Rightarrow\widehat{PCQ}=\widehat{PCI}=\frac{\widehat{QCI}}{2}=\frac{90^0}{2}=45^0\)
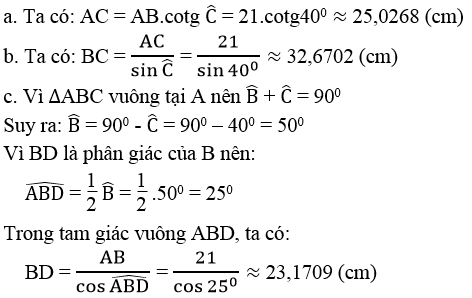
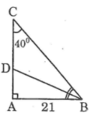

AC=AB/ tan \(40^0\) =25
BC=AB/sin \(40^0\) =32,6
góc B=\(90^0\) \(-\) \(40^0\) =\(50^0\)
=>Góc ABD=\(25^0\)
BD=AB/cos \(25^0\) =23,7