Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMBE vuông tại E và ΔNCF vuông tại F có
MB=CN
\(\widehat{MBE}=\widehat{NCF}\left(=\widehat{ACB}\right)\)
Do đó: ΔMBE=ΔNCF
Suy ra: ME=NF
Xét ΔMEI vuông tại E và ΔNFI vuông tại F có
ME=NF
\(\widehat{EMI}=\widehat{FNI}\)
Do đó: ΔMEI=ΔNFI\(\left(cgv-gnk\right)\)
Suy ra: IE=IF
b: Ta có: CD=CN
mà CN=MB
nên MB=DC
Xét ΔBAC có
\(\dfrac{MB}{BA}=\dfrac{CD}{AC}\)
nên MD//BC
Xét tứ giác BMDC có MD//BC
nên BMDC là hình thang
mà \(\widehat{MBC}=\widehat{DCB}\)
nên BMDC là hình thang cân

A C N M E F I B D
Hình nè,nhìn rồi giải nha

Xét ΔvEBM và ΔvFCN, ta có:
BM = CN (gt)
∠EBM = ∠FCN ( = ∠ACB )
=> ΔEBM = ΔFCN (ch-gn)
=> EM = FN ( cctứ )
Xét ΔvIEM và ΔvIFN, ta có:
EM = FN (cmt)
∠EMI = ∠FNI ( ∠EMI = 90° - ∠EIM = 90° - ∠FIN = ∠FNI )
=> ΔIEM = ΔIFN (cgv-gn)
=> IE = IF ( cctứ ) ( đpcm)

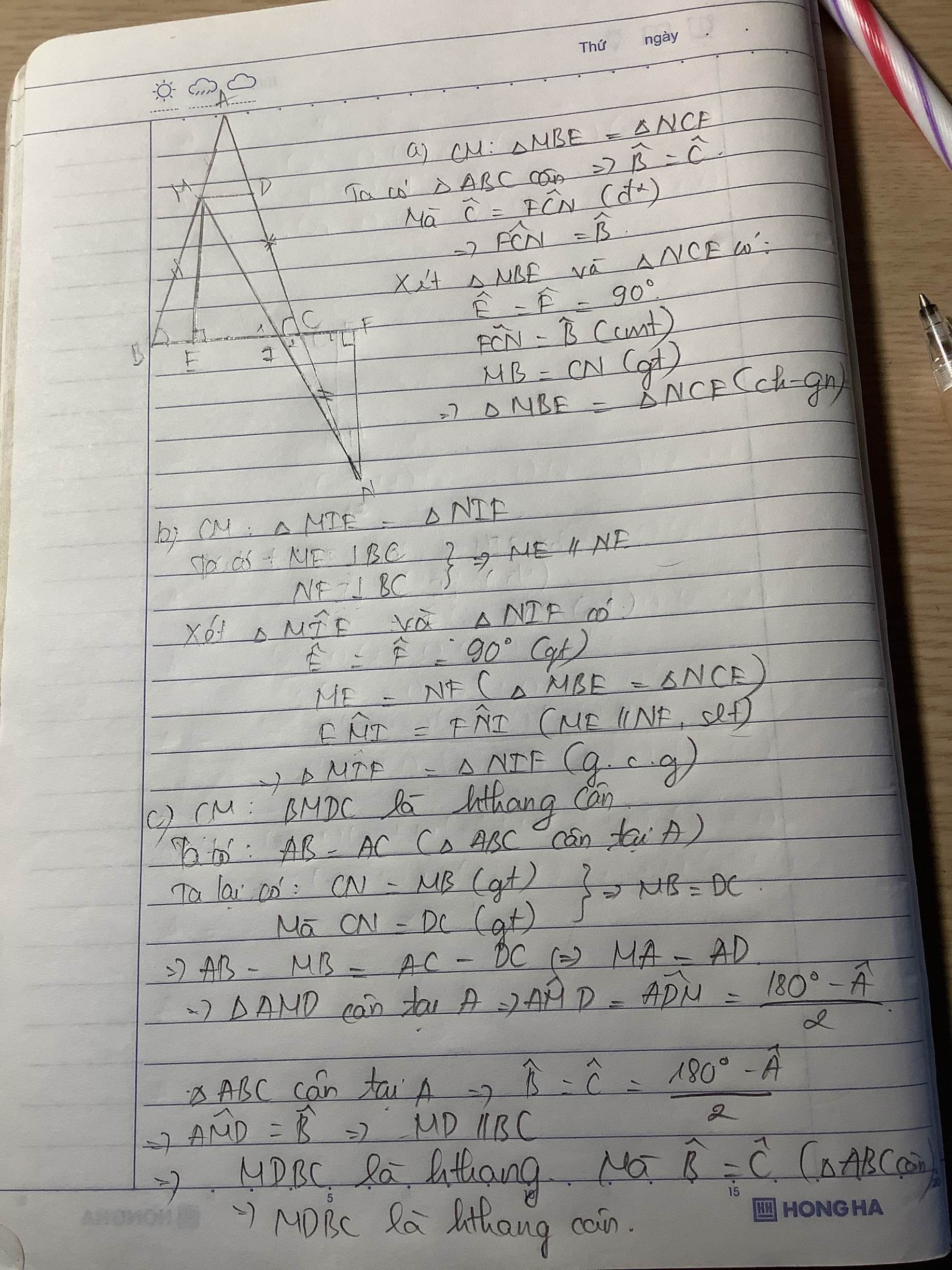
đề bài sai rồi bn ơi
Đâu có sai bạn