Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hướng dẫn:
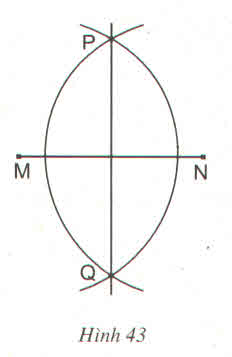
Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN
Hướng dẫn:

Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN

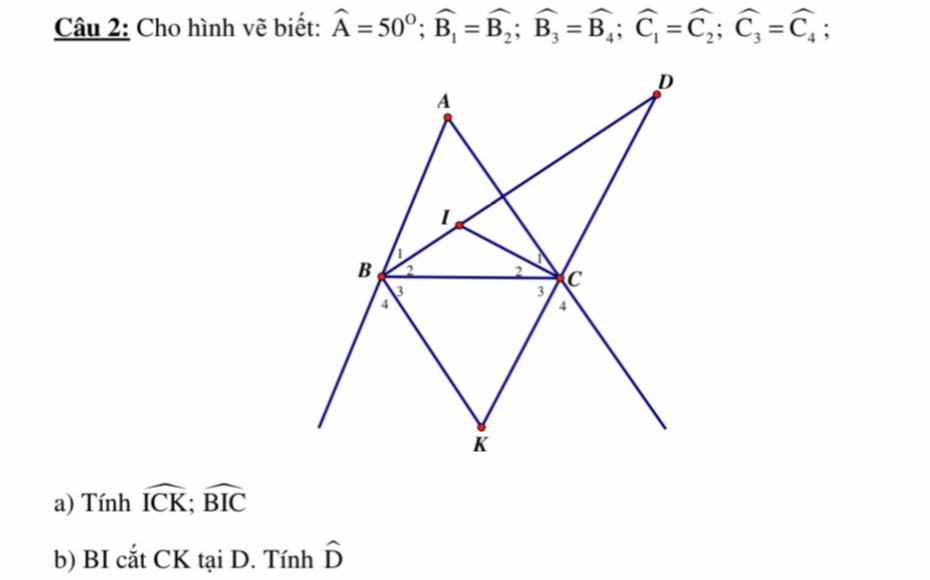
a. Gợi ý: \(\widehat{ICK}=\widehat{C_2}+\widehat{C_3}=\dfrac{1}{2}\left(\widehat{ACB}+\widehat{C}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
\(\widehat{BIC}=180^0-\left(\widehat{B_2}-\widehat{C_2}\right)=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-\dfrac{1}{2}\left(180^0-\widehat{BAC}\right)=180^0-90^0+\dfrac{1}{2}\widehat{BAC}=90^0+25^0=115^0\)
b. \(\widehat{ICK}=\widehat{D}+\widehat{CID}\Rightarrow\widehat{D}=90^0-\widehat{CID}=90^0-\left(180^0-\widehat{BIC}\right)=...\)

Hướng dẫn:

+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34

+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34


Ta có : AB=AC
=> \(\Delta ABC\) là tam giác vuông cân tại A ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{ABC}=A\widehat{CB}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{ABC}=A\widehat{CB}=45^0\)
=> \(\widehat{CBD}=\widehat{A}+\widehat{BCA}=135^0\) ( góc ngoài của tam giác )
Ta lại có:
BD=BC
=> \(\Delta BCD\) cân tại B ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{BDC}=\widehat{BCD}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{BDC}=\widehat{BCD}=\dfrac{\left(180^0-135^0\right)}{2}=\dfrac{45^0}{2}=22,5^0\)
Mà \(\widehat{ACD}=\widehat{BCA}+\widehat{BCD}\)
=> \(\widehat{ACD}=45^0+22,5^0=67,5^0\)
Vậy trong \(\Delta ACD\) có :
\(\left\{{}\begin{matrix}\widehat{A}=90^0\\\widehat{ADC}=22,5^0\\\widehat{ACD}=67,5^0\end{matrix}\right.\)