Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)

\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1}{\left(3y+3\right)^3}=\dfrac{1}{27y^3+81y^2+81y+27}\)
\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1^3}{\left(3y+3\right)^3}=\dfrac{1}{27\left(y^3+3y^2+3y+1\right)}\)

\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)

a,(x+2y)3 =x3+3.x2.2y+3.x.(2y)2+(2y)3
= x3+6x2y+12xy2+8y3
b, phần b tương tự dấu thay đổi một tí
c, (5x+1)(5x+1)= (5x+1)2
=25x2+10x+1


Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2

Giải:
a) \(\left(2x+y+3\right)^2\)
\(=\left(2x+y\right)^2+2.3\left(2x+y\right)+3^2\)
\(=\left(2x\right)^2+2.2x.y+y^2+2.3\left(2x+y\right)+3^2\)
\(=4x^2+4xy+y^2+12x+6y+9\)
Vậy ...
b) \(\left(x-2y+1\right)^2\)
\(=\left(x-2y\right)^2+2\left(x-2y\right)+1^2\)
\(=x^2-2.x.2y+\left(2y\right)^2+2x-4y+1^2\)
\(=x^2-4xy+4y^2+2x-4y+1\)
Vậy ...
c) \(\left(x^2-2xy^2-3\right)^2\)
\(=\left(x^2-2xy^2\right)^2+2.3.\left(x^2-2xy^2\right)-3^2\)
\(=\left(x^2\right)^2-2.x^2.2xy^2+\left(2xy^2\right)^2+2.3.\left(x^2-2xy^2\right)-3^2\)
\(=x^4-4x^3y^2+4x^2y^4+6x^2-12xy^2-9\)
Vậy ...
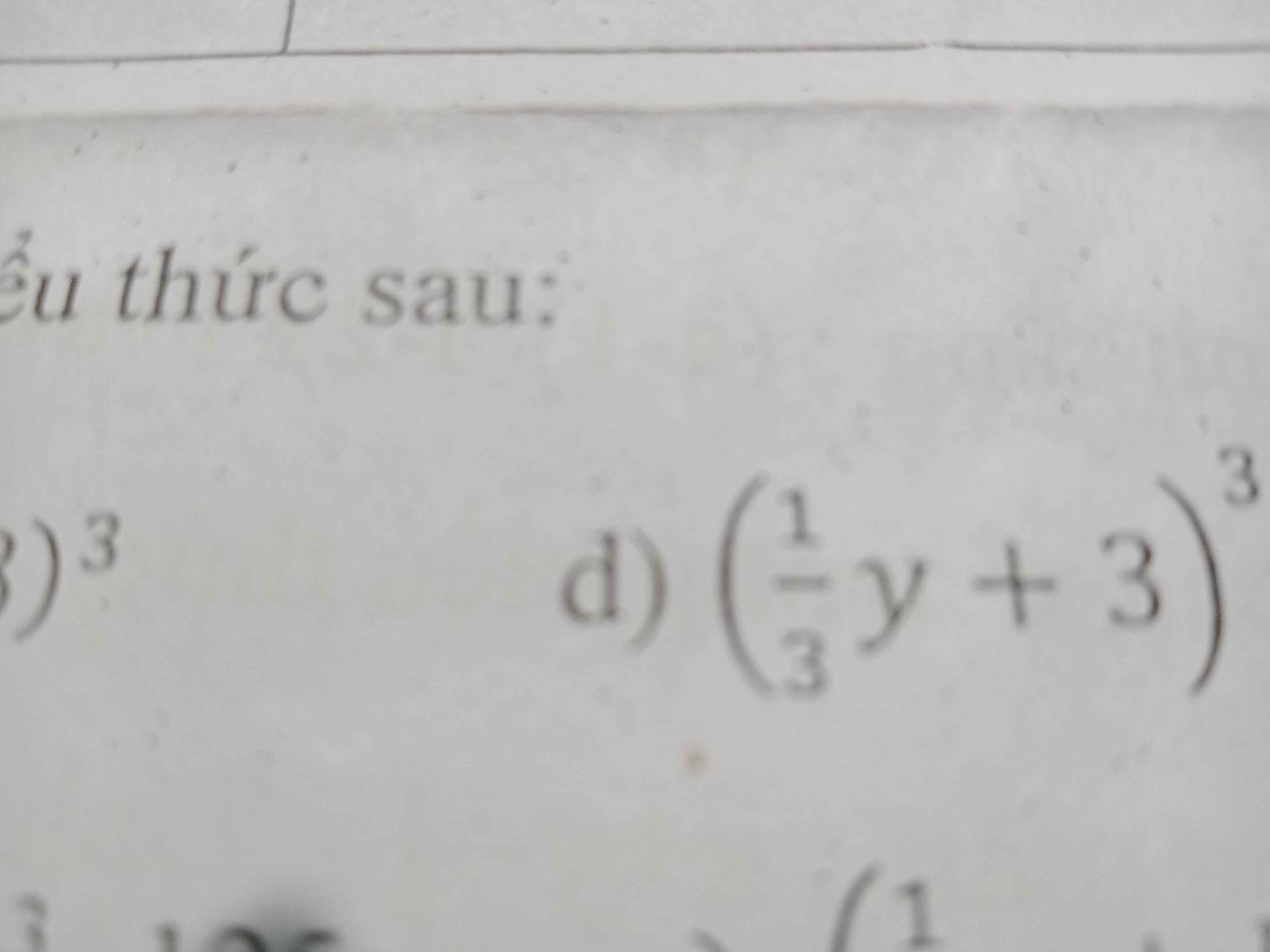
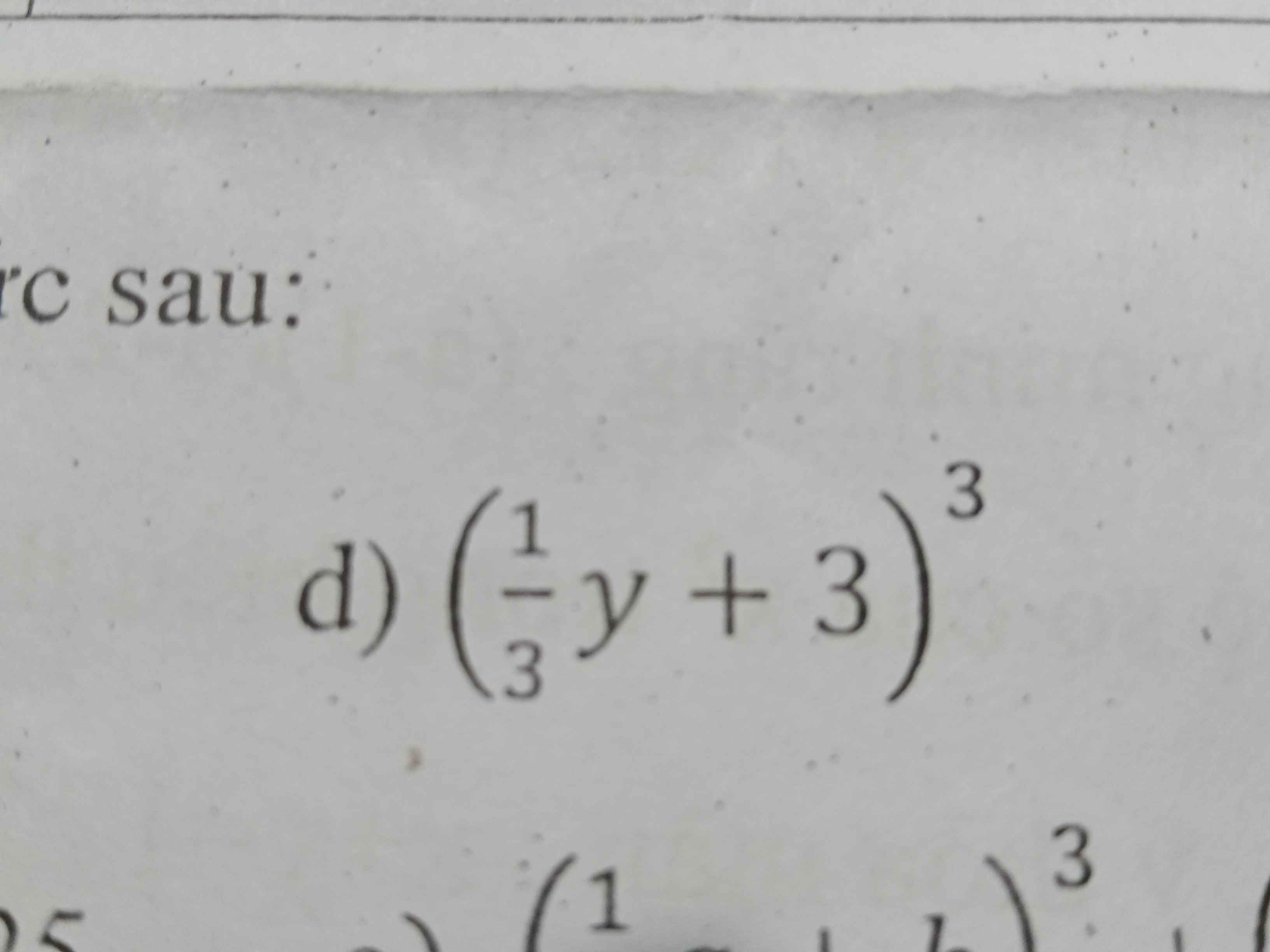

\(\left(x+y\right)^3=x^3+3x^2y+3xy^2-y^3\)
\(\left(x-y\right)^3=x^3-3x^2y+3xy^2-y^3\)
\(\left(2y-3\right)^3=8y^3-36y^2+54y-27\)
a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)