
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4) Ta có: ADB = BDC
Mà 2 góc này ở vị trí so le trong
=> AB//CD
Đúng thì like giúp mik nhé. Thx bạn
3) Dy//Ct vì \(\widehat{tCd}+\widehat{yDC}=180^0\) và \(\widehat{tCd}\); \(\widehat{yDC}\) là hai góc trong cùng phía


x y A C D O B E
Kéo dài CO sao cho CO cắt DB tại E
Ta chứng minh được \(\Delta AOC=\Delta BOE\left(g-c-g\right)\)
\(\Rightarrow\) OC=OE và AC=BE
Mà \(B\in DE\) => BE+BD=DE => AC+BD=DE (1)
Do OC=OE mà \(O\in CE\) => O là trung điểm của CE. Mà \(OD\perp OC\Rightarrow OD\perp CE\) => OD là trung trực của CE => CD=ED (2)
Từ (1) và (2) => AC+BD=CD
Vậy CD=AC+BD

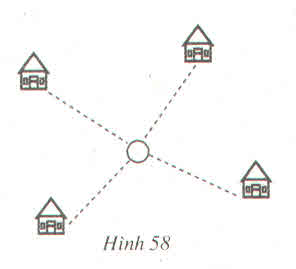
Gọi O là một điểm tùy ý (nơi phải đặt nhà máy) A, B, C, D lần lượt là bốn điểm dân cư.
Tổng khoảng cách từ nhà máy đến 4 khu dân cư là: OA + OB + OC + OD
Ta có:
Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà máy này đến các khu dân cư là ngắn nhất.
Gọi O là một điểm tùy ý (nơi phải đặt nhà máy) A, B, C, D lần lượt là bốn điểm dân cư.
Tổng khoảng cách từ nhà máy đến 4 khu dân cư là: OA + OB + OC + OD
Ta có:

Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà máy này đến các khu dân cư là ngắn nhất.

\(\frac{x}{-9}=\frac{y}{12}\text{ và }2.x-3.y=163\left(1\right)\)
\(\text{C1: Ta có: }\frac{x}{-9}=\frac{y}{12}=k\)
\(\Leftrightarrow x=-9.k\text{ }\text{ }\text{ }\text{ }\)
\(\Leftrightarrow y=12.k\)
\(\text{Thay x=-9k, y=12k vào (1), ta được: }\)
\(2.\left(-9\right).k-3.12.k=163\)
\(\Leftrightarrow-18.k-36.k=163\)
\(\Leftrightarrow k.\left(-18-36\right)=163\)
\(\Leftrightarrow k.\left(-54\right)=163\)
\(\Leftrightarrow k=\frac{163}{-54}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{163}{-54}.\left(-9\right)\\y=\frac{163}{-54}.12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{163}{6}\\y=\frac{326}{-9}\end{matrix}\right.\)
\(\text{Vậy }\left(x,y\right)=\frac{163}{6},\frac{326}{-9}\)
\(\text{C2: Ta có: }\frac{x}{-9}=\frac{y}{12}\Rightarrow\frac{2x}{-18}=\frac{3y}{36}\)
\(\Rightarrow\frac{2x}{-18}=\frac{3y}{36}=\frac{2x-3y}{-18-36}\left(2\right)\)
\(\text{Thay (1) vào (2), ta được: }\)
\(\Rightarrow\frac{2x}{-18}=\frac{3y}{36}=\frac{2x-3y}{-18-36}=\frac{163}{-54}\)
\(\left(\text{Chỗ này bạn có thể thay luôn vào dòng trên không cần phải ghi cái dòng trên là thay đâu}\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{x}{-9}=\frac{163}{-54}\\\frac{y}{12}=\frac{163}{-54}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{163}{-54}.\left(-9\right)\\y=\frac{163}{-54}.12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{163}{6}\\y=\frac{326}{-9}\end{matrix}\right.\)
\(\text{Vậy }\left(x,y\right)=\frac{163}{6},\frac{326}{-9}\)

A B C D E H M
a) Xét hai tam giác AMB và DMC có:
MA = MD (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
MB = MC (do AM là đường trung tuyến)
Vậy: \(\Delta AMB=\Delta DMC\left(c-g-c\right)\)
Suy ra: AB = CD (hai cạnh tương ứng)
Mà AC > AB (gt)
\(\Rightarrow\) AC > AD
\(\Delta DAC\) có AC > AD \(\Rightarrow\widehat{ADC}>\widehat{DAC}\) (quan hệ giũa góc và cạnh đối diện trong tam giác).
b) \(\Delta ABC\) có: AC > AB (gt)
\(\Rightarrow\) HB > HC (quan hệ giữa đường xiên - hình chiếu)
\(\Delta EBC\) có: HC > HB (cmt)
\(\Rightarrow\) EC > EB (quan hệ giữa đường xiên - hình chiếu).
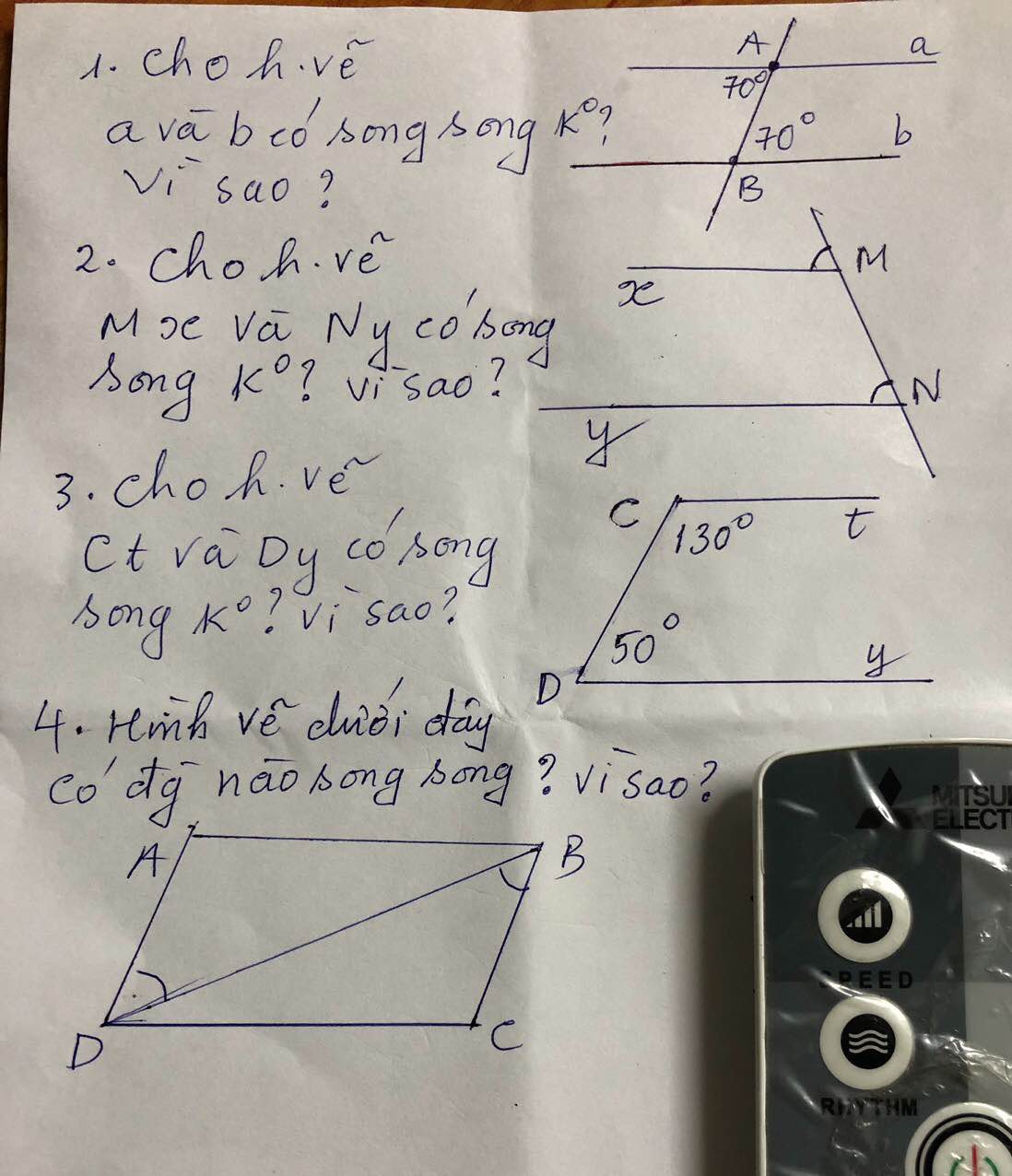
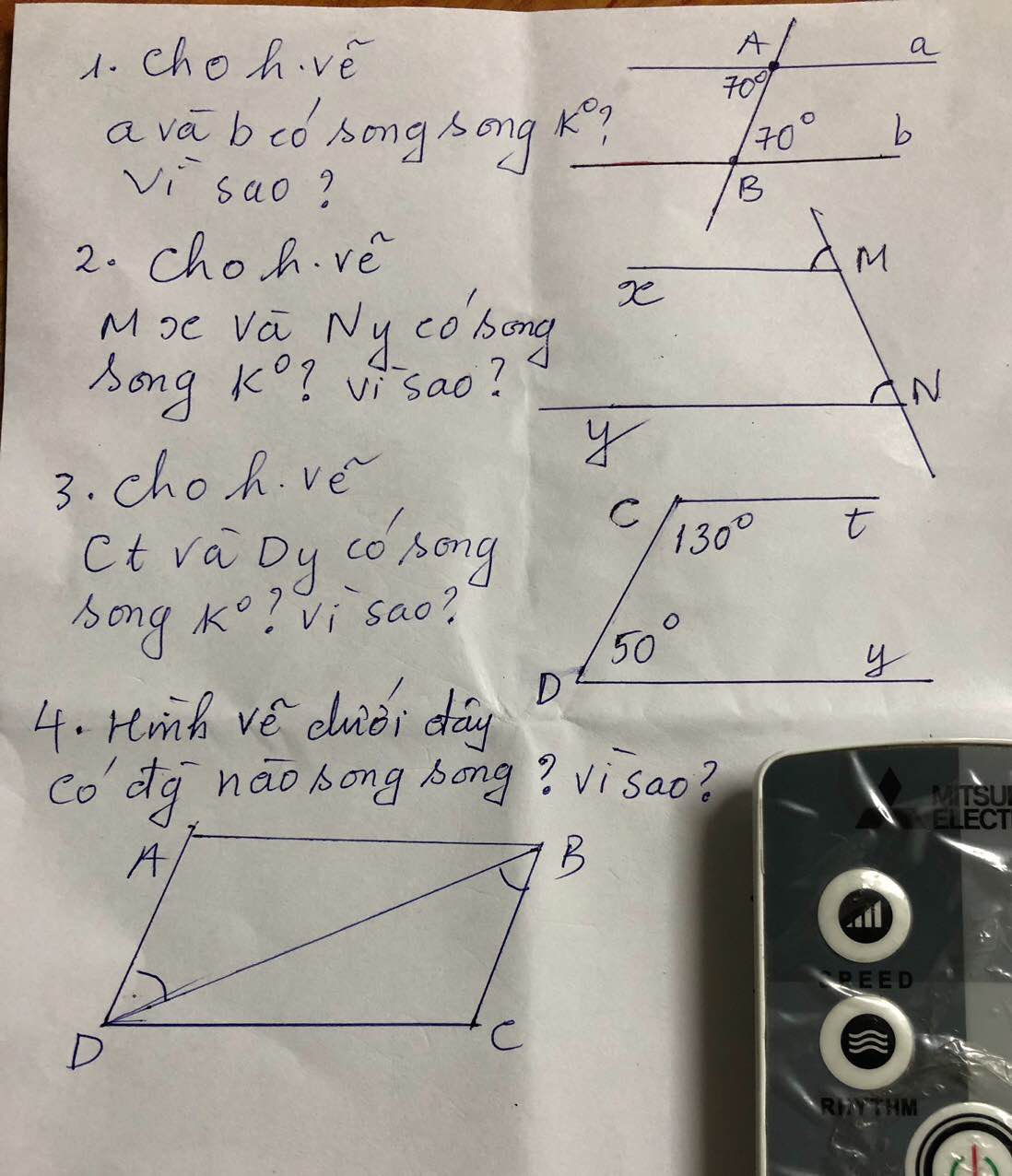

1, a và b có song song vì \(\)có 2 góc =70 độ ở vị trí so le trong
2.Mx và Ny có song song do góc M =góc N và 2 góc ở vị trí đônhg vị
3.Ct và Dy có song song vì góc C+ góc D=180 độ và 2 góc này ở vị trí trong cùng phía
4. có AD song song BC vì góc ADB=góc DBC
và 2 góc ở vị trí so le trong
4:
Có: Góc ADB = Góc DBC (GT)
Mà 2 góc này là 2 góc so le trong
=> AD // BC