Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{x_2}{x_1}=\dfrac{x_3}{x_2}=\dfrac{x_2+x_3}{x_1+x_2}=\dfrac{x_2+x_3}{3}\) (1)
\(\dfrac{x_3}{x_2}=\dfrac{x_4}{x_3}=\dfrac{x_3+x_4}{x_2+x_3}=\dfrac{12}{x_2+x_3}\)
\(\Rightarrow\dfrac{x_2+x_3}{3}=\dfrac{12}{x_2+x_3}\Rightarrow x_2+x_3=\pm6\)
Th1: \(x_2+x_3=6\) thế vào (1):
\(\dfrac{x_2}{x_1}=\dfrac{x_3}{x_2}=\dfrac{x_4}{x_3}=\dfrac{6}{3}=2\) \(\Rightarrow\left\{{}\begin{matrix}x_2=2x_1\\x_4=2x_3\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}x_1+x_2=3\\x_3+x_4=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3x_1=3\\3x_3=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=1;x_2=2\\x_3=4;x_4=8\end{matrix}\right.\)
\(\Rightarrow m=x_1x_2=2\)
Khỏi cần làm TH2 \(x_2+x_3=-6\) nữa, chọn luôn C

a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
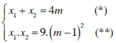
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
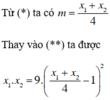
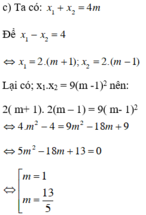
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành 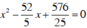 có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.

Đáp án: A
![]()
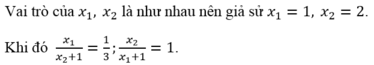
Ta tìm phương trình có 2 nghiệm là ![]() và 1. Ta có thể thử nghiệm vào từng phương trình xem phương trình nào thỏa mãn hoặc giải từng phương trình rồi so sánh nghiệm.
và 1. Ta có thể thử nghiệm vào từng phương trình xem phương trình nào thỏa mãn hoặc giải từng phương trình rồi so sánh nghiệm.

⇒ Chọn đáp án A.

Hình như đề thiếu, pt: \(x^2-\left(m+1\right)x+m-2=0\)
Phương trình đã cho có nghiệm khi \(\Delta=\left(m+1\right)^2-4\left(m-2\right)=m^2-2m+9>0\)
\(\Rightarrow\) Phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị m
Định lí Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m-2\end{matrix}\right.\)
a, Theo giả thiết ta có: \(x_1^2+x_2^2=100\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=100\)
\(\Leftrightarrow\left(m+1\right)^2-2\left(m-2\right)=100\)
\(\Leftrightarrow m^2+2m+1-2m+4=100\)
\(\Leftrightarrow m^2=95\)
\(\Leftrightarrow m=\sqrt{95}\)
b, \(P=\left|x_1-x_2\right|\)
\(P^2=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=\left(m+1\right)^2-4\left(m-2\right)\)
\(=m^2-2m+9=\left(m-1\right)^2+8\ge8\)
\(\Rightarrow P=\left|x_1-x_2\right|\ge2\sqrt{2}\)
\(minP=2\sqrt{2}\Leftrightarrow m=1\)

a: Để phương trình có hai nghiệm trái dấu thì m+2<0
hay m<-2

Theo định lí Viet thì \(\left\{{}\begin{matrix}x_1+x_2=4m\\x_1.x_2=\left(3m-3\right)^2\end{matrix}\right.\)
\(\dfrac{16}{9}.x_1.x_2=\dfrac{16}{9}.\left(3m-3\right)^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left[\dfrac{4}{3}.\left(3m-3\right)\right]^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left(4m-4\right)^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left(x_1+x_2-4\right)^2\)
Đối chiếu ⇒ \(\left\{{}\begin{matrix}a=-4\\b=\dfrac{16}{9}\end{matrix}\right.\)
⇒ \(\dfrac{b}{a}=\dfrac{-4}{9}\)

Trước hết phải xét điều kiện để phương trình x 2 - 2 m - 1 x + m 2 - 3 m + 4 = 0 có nghiệm: ∆ ' = m - 1 2 - m 2 - 3 m + 4 = m - 3 > 0 hay m > 3.
Từ đó thấy ngay các phương án A, B, C đều sai.
Khi m = 4 thì phương trình đã cho có 2 nghiệm .
Áp dụng hệ thức Vi- et ta có:
x 1 + x 2 = 2 m - 1 = 2 . 4 - 1 = 6 x 1 . x 2 = m 2 - 3 m + 4 = 4 2 - 3 . 4 + 4 = 8
Khi đó; x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 . x 2 = 6 2 - 2 . 8 = 20