
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




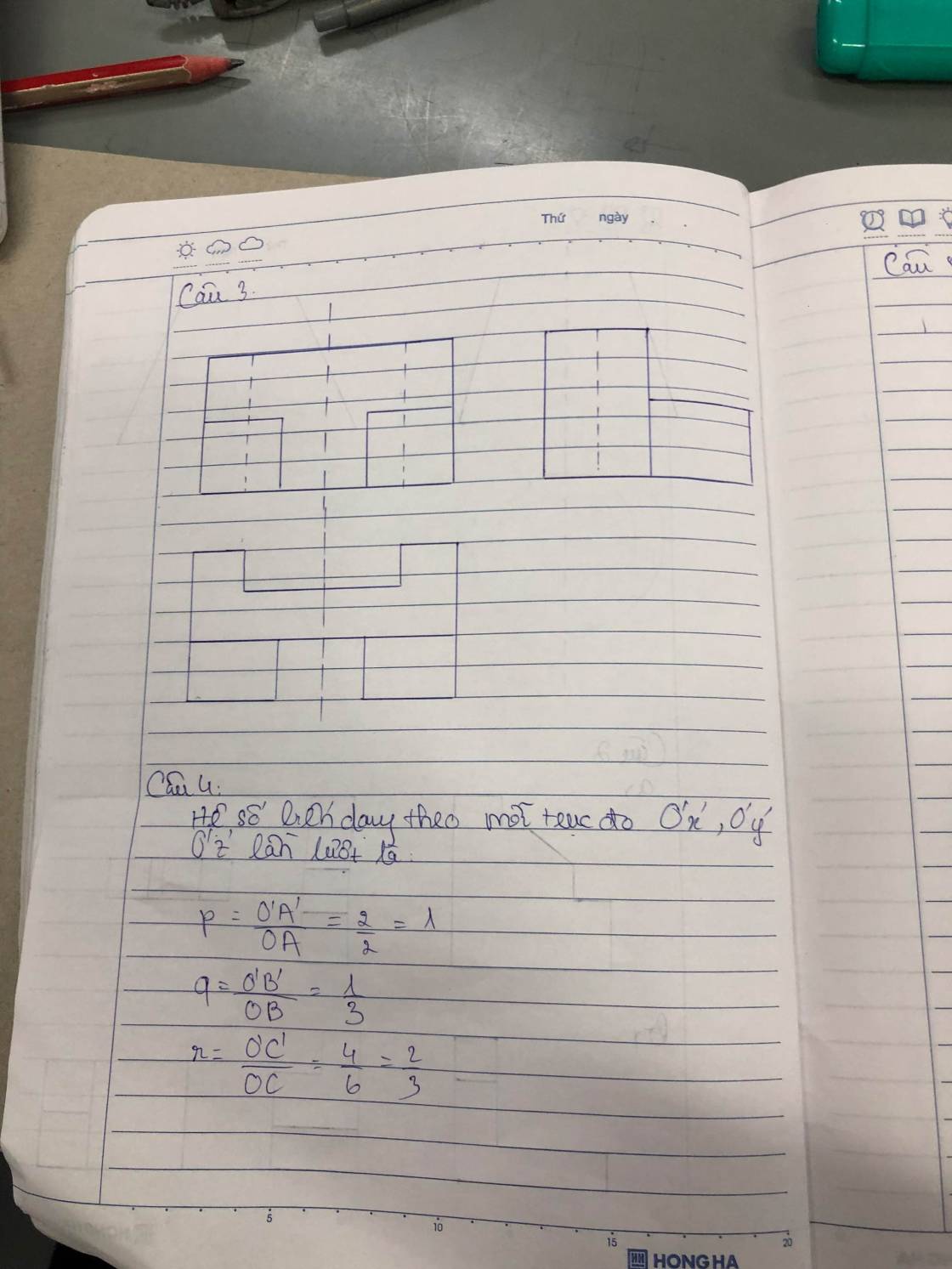
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.

a)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).


a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
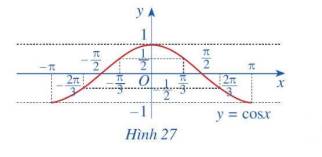
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
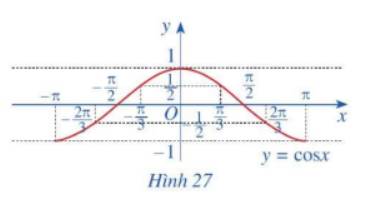
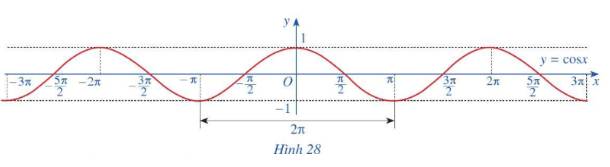
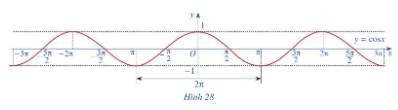
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

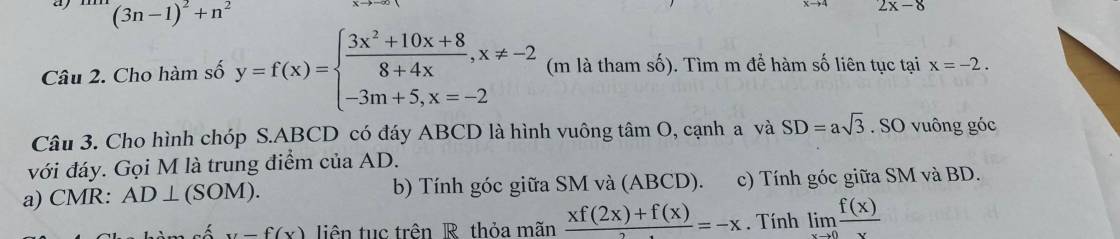


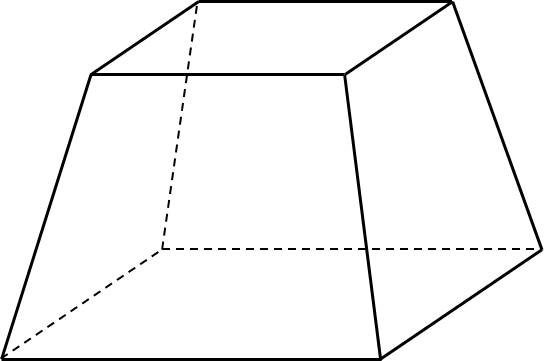
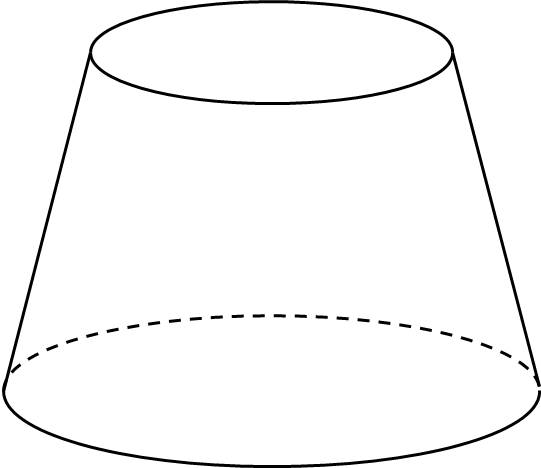
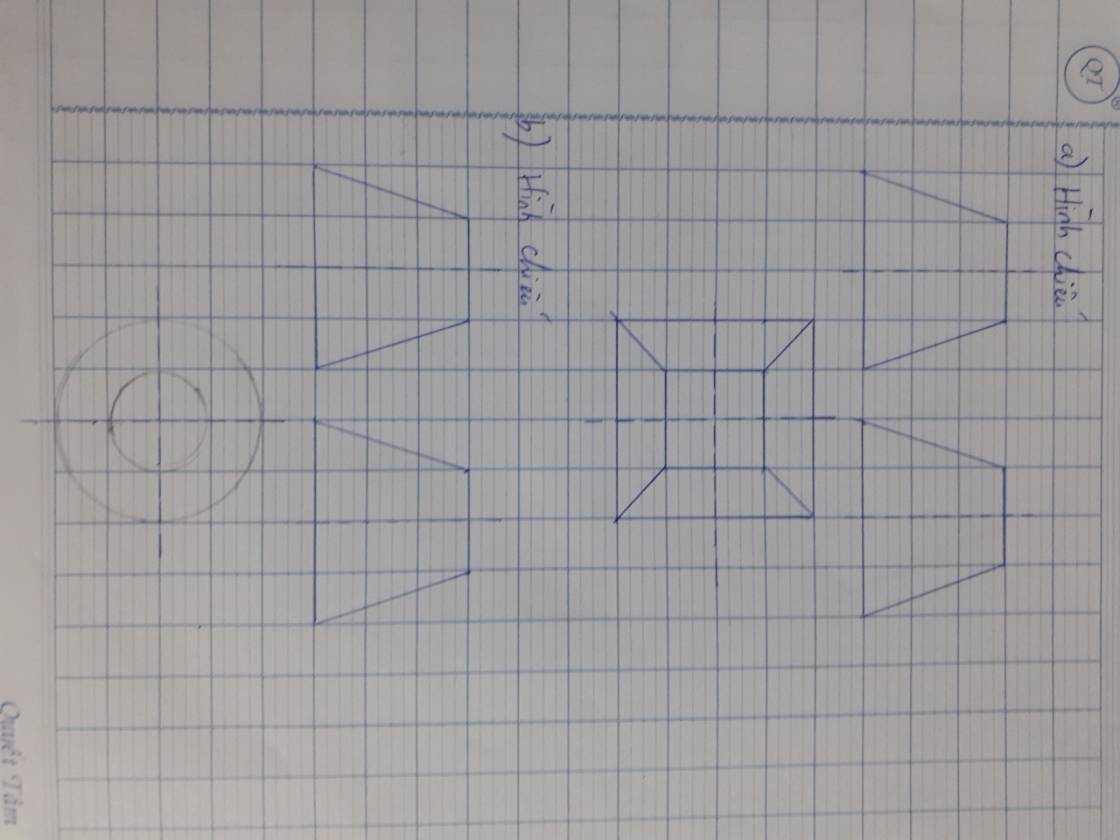
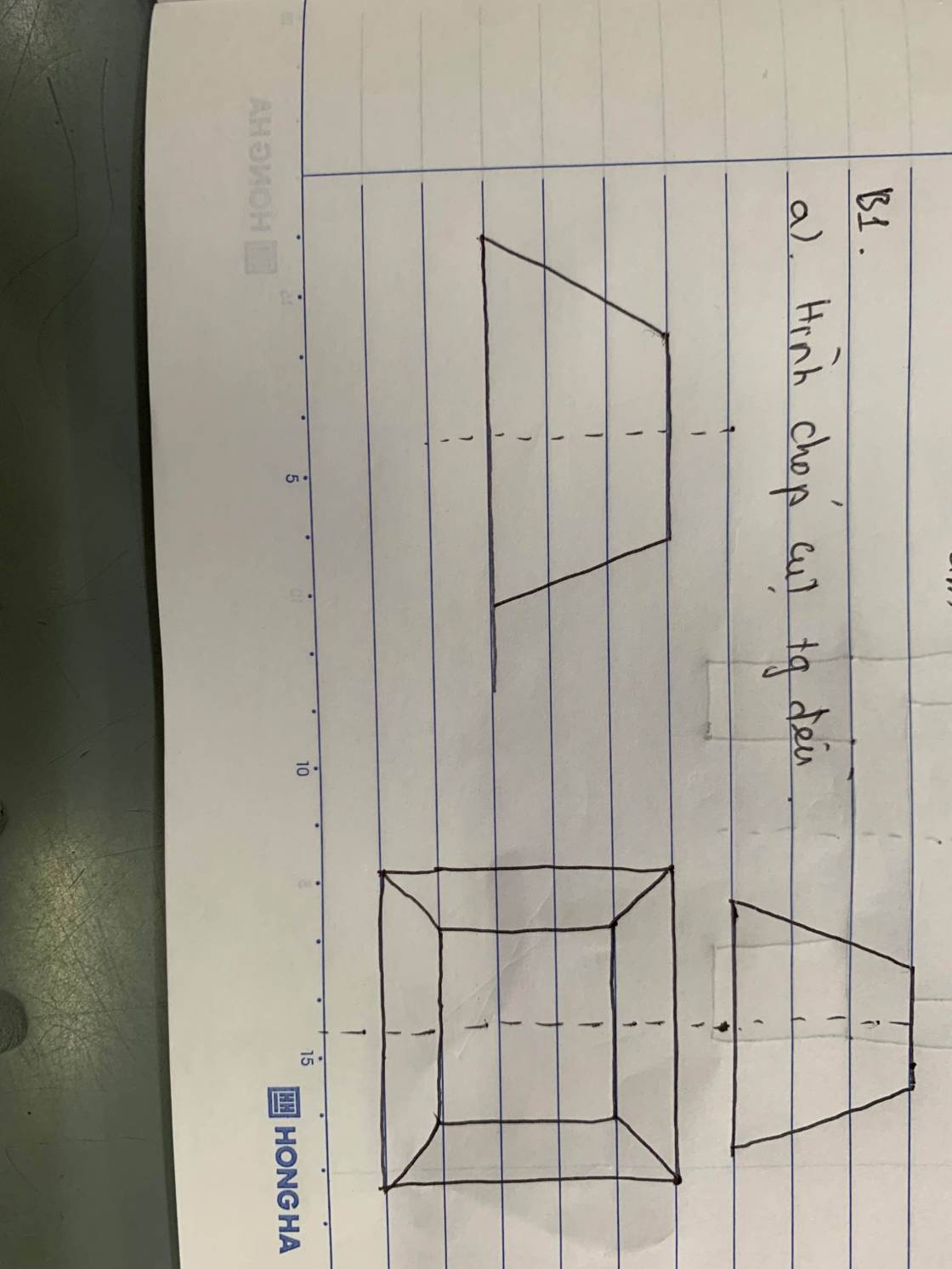
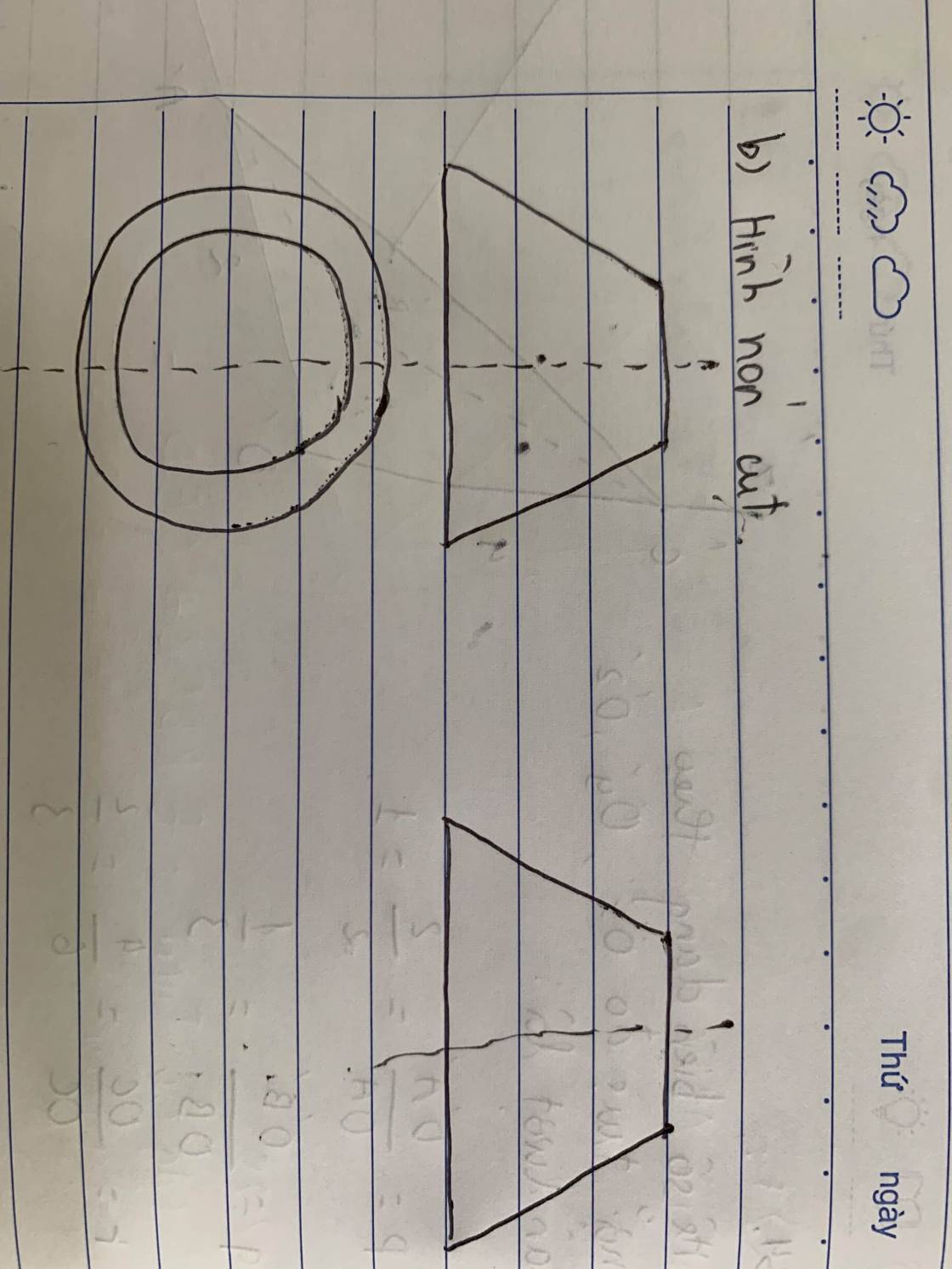





 giúp t với ạ
giúp t với ạ
 giúp mình với ạ
giúp mình với ạ
 Giúp e vs ạ
Giúp e vs ạ
b.
\(SO\perp\left(ABCD\right)\Rightarrow OM\) là hình chiếu vuông gốc của SM lên (ABCD)
\(\Rightarrow\widehat{SMO}\) là góc giữa SM và (ABCD)
\(BD=a\sqrt{2}\Rightarrow SO=\sqrt{SD^2-OD^2}=\sqrt{3a^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{10}}{2}\)
\(OM=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow tan\widehat{SMO}=\sqrt{10}\Rightarrow\widehat{SMO}=...\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(SM;BD\right)}=\widehat{\left(SM;MN\right)}=\widehat{SMN}\)
\(OM=ON\Rightarrow SN=SM=\sqrt{SO^2+OM^2}=\dfrac{a\sqrt{11}}{2}\)
Định lý hàm cos:
\(cos\widehat{SMN}=\dfrac{SM^2+MN^2-SN^2}{2SM.MN}=\dfrac{\sqrt{22}}{22}\Rightarrow\widehat{SMN}=...\)