Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAOC và ΔBOC có
OA=OB
OC chung
AC=BC
Do đó: ΔAOC=ΔBOC

a: Xét ΔAOC và ΔBOC có
OA=OB
OC chung
AC=BC
Do đó: ΔAOC=ΔBOC

a: Xét ΔAOC và ΔBOC có
OA=OB
CA=CB
OC chung
Do đó: ΔOAC=ΔOBC
b: ΔOAC=ΔOBC
=>\(\widehat{AOC}=\widehat{BOC}\)
=>OC là phân giác của \(\widehat{xOy}\)

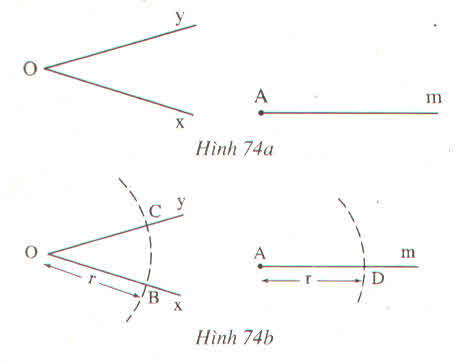
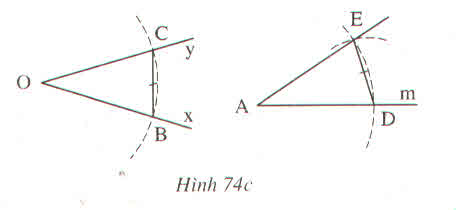
Tam giác DAE và BOC có:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
Nên ∆ DAE= ∆ BOC(c.c.c)
suy ra \(\widehat{DAE}\)=\(\widehat{BOC}\)(hai góc tương tứng)
vậy
\(\widehat{DAE}\)=\(\widehat{xOy}\).

a, Vì Oz là tia phân giác của xOy
=> xOz = zOy = xOy/2 = 60o/2 = 30o
b, Xét △OIA và △ OIB
Có: OA = OB
AOI = IOB
OT là cạnh chung
=> △OIA = △OIB (c.g.c)
c, Vì △OIA = △OIB
=> AIO = OIB (2 góc tương ứng)
Mà AIO + OIB = 180o (2 góc kề bù)
=> AIO = OIB = 90o
=> OI vuông góc AB
Hình dễ tự vẽ
a ) Oz là tia p/g của góc xOy => \(\widehat{xOz}=\widehat{zOy}=\frac{1}{2}.\widehat{xOy}=30^o\)
=> góc zOy = 30 độ
b ) Xét tam giác OIA và tam giác OIB có :
OA = OB ( gt )
\(\widehat{xOz}=\widehat{zOy}\)( Oz là tia p/g của góc xOy )
OI là cạnh chung
=> Tam giác OIA = Tam giác OIB ( c.g.c )
b ) Do tam giác OIA = tam giác OIB ( cm trên ) => \(\widehat{OIA}=\widehat{OIB}\)
Ta có :
\(\widehat{OIA}+\widehat{OIB}=180^o\)( hai góc kề bù )
\(\widehat{OIA}+\widehat{OIA}=180^o\)
\(\widehat{OIA}.2=180^o\)
=> \(\widehat{OIA}=90^o\)
=> OI vuông góc với AB
O x y A B
Vì trong cùng một đường tròn, các bán kính đều bằng nhau nên OA = OB (1)
\(\widehat{xOy}=60^0\) (2)
Từ (1) và (2) \(\Rightarrow\Delta AOB\) đều.
Okay !