Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cùng chiều : F=F1+F2=7 N.
ngược chiều :F=|F1-F2|=1 N (Hợp lực ở đây có cùng chiều với F2).
tạo với nhau 1 góc 120 độ :F2=F12+F22+2*F1*F2*cos(120) = \(\sqrt{13}\) N.
Còn nếu muốn có gia tốc thì bạn phải cho khối lượng chứ .

F=\(\sqrt{F^2_1+F_2^2+2F_1.F_2.\cos\alpha}\)\(\Rightarrow\)F2=0N

mình muốn hỏi là ở câu b có F=3,5N mà Fmin=4. Vậy tại sao F>Fmin ???

1.
Ta thấy: \({10^2} = \sqrt {{6^2} + {8^2}} \Rightarrow {F^2} = \sqrt {F_1^2 + F_2^2} \)
Suy ra \({F_1} \bot {F_2}\)
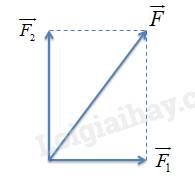
2.
a)
Biểu diễn các lực kéo của mỗi tàu và hợp lực tác dụng vào tàu chở hàng:
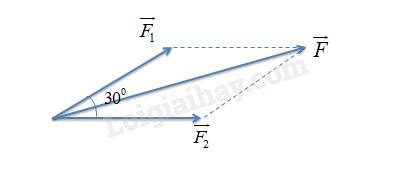
b)
Độ lớn của hợp lực là:
\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \left( {{F_1},{F_2}} \right)} \)
\( \Leftrightarrow F = \sqrt {{{8000}^2} + {{8000}^2} + 2.8000.8000.\cos {{30}^0}} \)
\( \Leftrightarrow F = 15455\left( N \right)\)
c)
Hợp lực có:
- Chiều: hướng về phía trước
- Phương: hợp với \(\overrightarrow {{F_1}} \) góc \({15^0}\)
d) Nếu góc giữa hai dây cáp bằng \({90^0}\) thì hợp lực có:
- Phương: xiên
- Chiều hướng sang trái hoặc phải.
- Độ lớn: \(F = \sqrt {F_1^2 + F_2^2} \)

\(cos\alpha=\dfrac{F_1^2+F_2^2-F^2}{2.F_1.F_2}\)\(\Rightarrow\)\(\alpha\)\(\approx\)1190

Ta có: \(F_1=ma_1\)
\(F_2=2F_1=ma_2\)
Có tỉ số sau : \(\frac{F_1}{F_2}=\frac{F_1}{2F_1}=\frac{ma_1}{ma_2}=\frac{1}{2}\)
=> \(\frac{a_1}{a_2}=\frac{1}{2}\)
=> \(a_2=2a_1\)

\(F_1=F.\cos30=\frac{60.\sqrt{3}}{2}=30\sqrt{3}\left(N\right)\)
\(F_2=F.\cos60=\frac{60.1}{2}=30\left(N\right)\)
Muốn thử lại xem đúng hay ko áp dụng định lý hàm sin
\(F^2=F_1^2+F_2^2+2F_1F_2.\cos\left(\widehat{F_1;F_2}\right)\)
Chắc chắn đúng =))
Tặng kèm cái hình


Câu 9: một vật rắn cân bằng dưới tác dụng của ba lực có độ lớn F1 = 6N, F2 = 8N, F3 = 10N. Nếu bỏ đi lực F2 thì hợp của hai lực còn lại có độ lớn
A. 10N
B. 8N
C. 16N
D. 14N
giải thích các bước giải cho tớ được ko ạ :(