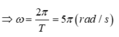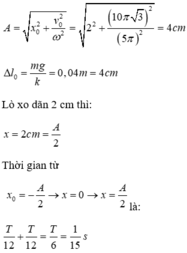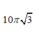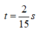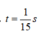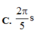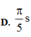Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có ∆l = mg/k = 0,025 m = 2,5 cm.
![]()
![]()
![]()
→ quãng thời gian ![]() ngược chiều nhau là T/6 →
ngược chiều nhau là T/6 →
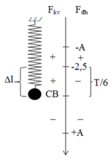 vật
vật
đi từ vị trí π/2 đến 2π/3 và -2π/3 đến –π/2.
→ -A/2 = 2,5 cm.
→ A = 5 cm.

W=√(g/dentaLo)=5√10
=>T=0,4s. Tại t=0,4/3=T/3 vật ở vt A/2=1cm. =>Fdh=KdentaL=K(dentalo-1)=3N

Đáp án A
+ Ta tính được
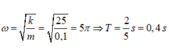
+ Độ biến dạng của lò xo khi vật ở vị trí cân bằng là
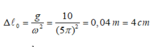
+ Từ VTCB, nâng vật lên 2 cm, tức là vật cách vị trí cân bằng 2 cm, suy ra |x| = 2 cm.
Áp dụng hệ thức liên hệ ta tính được biên độ dao động
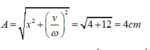
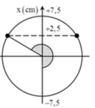
+ Sơ đồ chuyển động của vật được minh họa trên hình vẽ. Từ đó thay thấy thời điểm mà lúc vật qua vị trí lò xo dãn 6 cm lần hai (ở li độ x = 2 cm lần hai) là
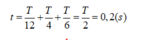

Đáp án A
Phương pháp: Sử dụng đường tròn lượng giác và lí thuyết về con lắc lò xo treo thẳng đứng
Cách giải:
- Độ dãn của lò xo khi vật ở vị trí cân bằng:
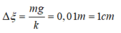
- Kéo vật xuống khỏi vị trí cân bằng theo phương thẳng đứng 2 cm rồi buông nhẹ nên biên độ dao động của vật: A = 2cm.
- Chu kỳ dao động T = 0,2s.
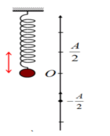
- Lò xo bị nén khi vật di chuyển trong đoạn từ li độ -1cm và biên âm -2cm, được biểu diễn bằng phần tô đậm như hình vẽ.
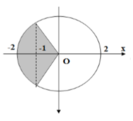
- Trong 0,5s = 2,5T, thời gian lò xo bị nén là: 2T/3 + T/6 = 1,6 (s)

Giải thích: Đáp án D
Phƣơng pháp: Sử dụng hệ thức độc lập theo thời gian của x và v
Cách giải:
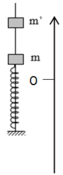
- Nếu không tác dụng lực vật sẽ dao động với biên độ A1 = 1 cm
- Khi có lực tác dụng VTCB dịch đi theo hướng lực tác dụng đoạn
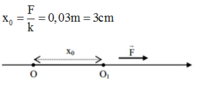
- Nên ngay khi thả vật sẽ dao động với biên độ A2 = A1 + x0 = 4 cm
- Chu kì dao động của vật là: 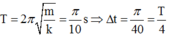
- Sau khi thả vật đi đến VTCB O1, lúc này vật có vận tốc là v2max = ωA2 = 80 cm/s
- Lúc này mất lực nên VTCB lại về O => lúc này vật có li độ là x = 3 cm nên dao động với biên độ là:
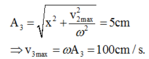
Chọn D