
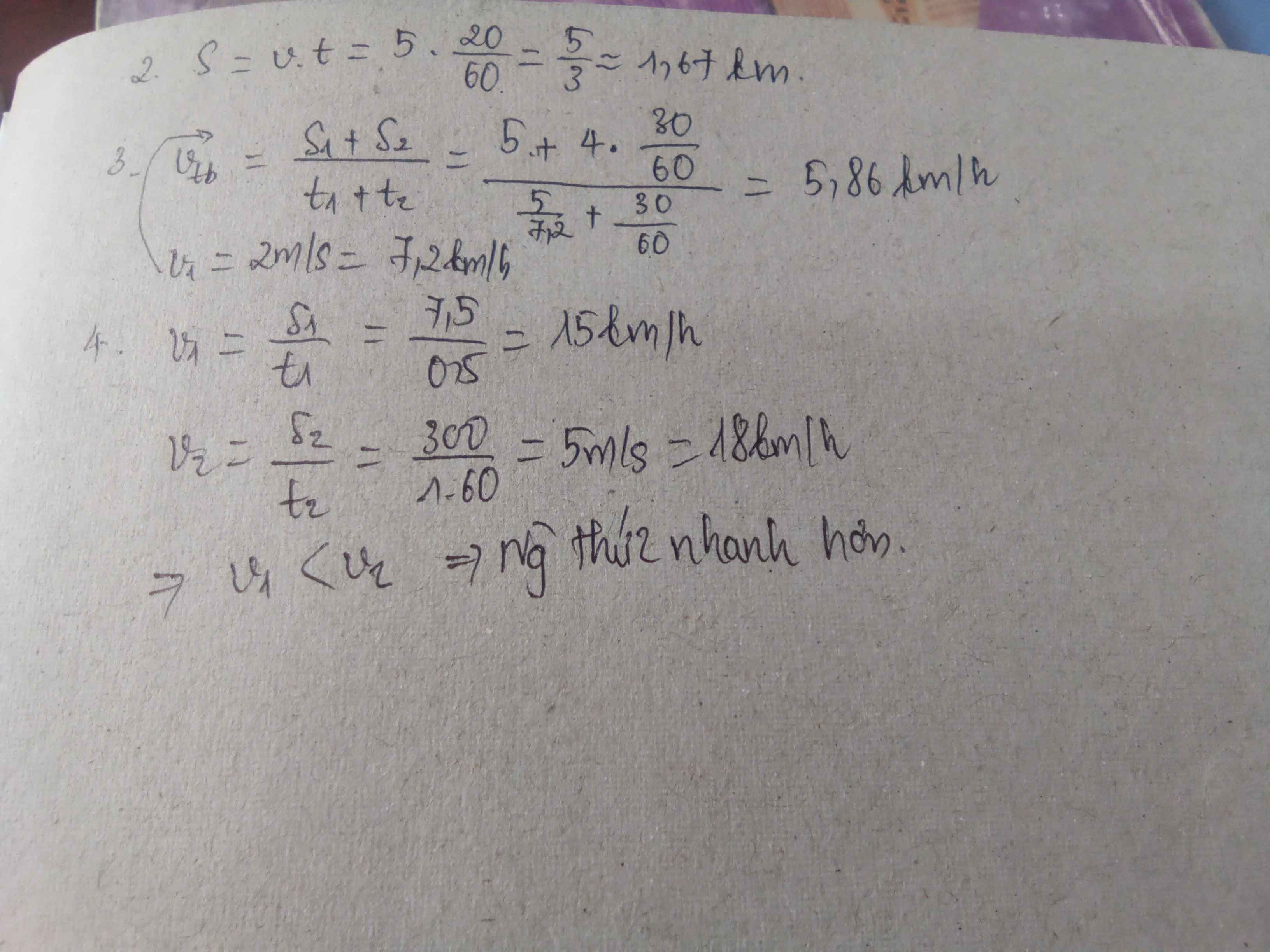
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

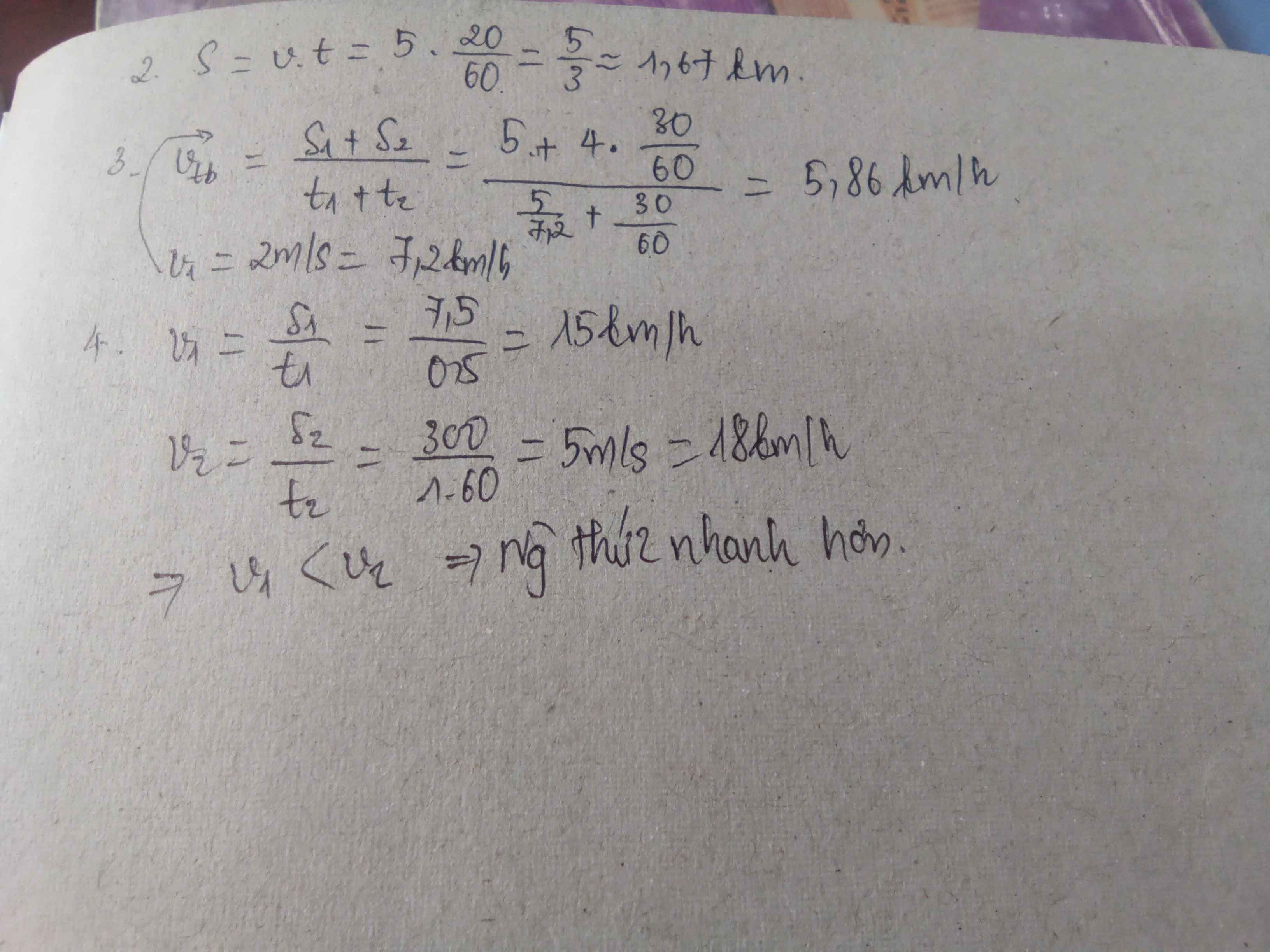
![]()

Bài 1: Tóm tắt
\(S_1=24km\)
\(V_1=12km\)/\(h\)
\(S_2=12km\)
\(V_2=45'=0,75h\)
_______________
a) \(t_1=?\)
b) \(V_{TB}\)
Giải
a) Thời gian người đó đạp xe trên quãng đường đầu là: \(t_1=\frac{S_1}{V_1}=\frac{24}{12}=2\left(h\right)\)
b) Ta có công thức tính vận tốc trung bình là: \(V=\frac{S_1+S_2+....+S_n}{t_1+t_2+t_3+....+t_n}\)
Vậy vận tốc trung bình của người đó trên quãng đường là:
\(V_{TB}=\frac{S_1+S_2}{t_1+t_2}=\frac{24+12}{2+0,75}\approx13\)(km/h)
Bài 2: Tóm tắt
\(S_1=600m=0,6km\)
\(t_1=2'=\frac{1}{30}\left(h\right)\)
\(S_2=10,8km\)
\(t_2=0,75h\)
_________________
a) \(V_1=?;V_2=?\)
b) \(S_{KC}=?\)
Giải
a) Vận tốc của người thứ nhất là: \(V_1=\frac{S_1}{t_1}=\frac{0,6}{\frac{1}{30}}=18\)(km/h)
Vận tốc của người thứ 2 là: \(V_2=\frac{S_2}{t_2}=\frac{10,8}{0,75}=14,4\) (km/h)
=> Người thứ nhất đi nhanh hơn người thứ 2.
b) Do đi cùng lúc => thời gian đi của 2 người là như nhau và vận tốc đã cho
=> Hai người cách nhau số km là: \(S-t\left(V_1+V_2\right)=S-\frac{1}{3}\left(18+14,4\right)=S-10,8\)
Theo đề thì còn cần phải dựa vào khoảng cách của 2 người khi 2 người bắt đầu đi nữa.
a) Thời gian người đó đạp xe trên quãng đường thứ nhất là :
24 : 12 = 2 (giờ)
b) Đổi : 45 phút = 0,75 giờ
=> Vận tốc trung bình của người đi xe đạp trên cả quãng đường là :
(S1 + S2) / (t1 + t2) = (12+24) / (2+0,75) = 13 (km/h)

\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_s}=\dfrac{6+\left(2.0,5\right)}{\dfrac{6}{5}+0,5}\approx4,1\left(km/h\right)\)

Bài 1:
Đổi \(40p=\dfrac{2}{3}h\)
Ta có: \(v=\dfrac{s}{t}\Leftrightarrow s=vt=\dfrac{12.2}{3}=8\left(km\right)\)
Bài 2:
Đổi \(30p=0,5h\)
Ta có: \(v=\dfrac{s}{t}\Leftrightarrow s=vt=4.0,5=2\left(km\right)\)
Bài 3:
Thời gian ô tô đi: 10-8 = 2h
Vận tốc của ô tô:
\(v=\dfrac{s}{t}=\dfrac{100}{2}=50\left(km/h\right)\)
Ta có: \(50km/h=\dfrac{50000}{3600}=13,89\left(m/s\right)\)

\(2\)m/s=7,2km/s
Thời gian người đó đi quãng đường thứ nhất : \(t=\dfrac{s}{v}=\dfrac{3}{7,2}=\dfrac{4}{5}\left(h\right)\)
Vận tóc TB của 2 quãng đường : \(v_{tb}=\dfrac{s+s'}{t+t'}=\dfrac{3+1,95}{\dfrac{4}{5}+0,5}\approx3,53\)(km/h)
đổi 3 km = 0,003 m
Thời gian người đi bộ đầu tiên là
\(t=\dfrac{s}{v}=0,003:2=0,0015\left(s\right)\)
đổi 0,0015 s = 0,0000004 h
Vận tốc trung bình của người đó trên cả 2 quãng đường là
\(V_{tb}=\dfrac{S+S_1}{t+t_1}=\dfrac{3+1,95}{0,5+0,0000004}=\dfrac{4,95}{0,5000004}=9,8\left(kmh\right)\)

Thời gian người đó đi từ A đến B là:
t = 8h5’ – 7h20’ = 45’ = 2700s
Quãng đường từ A đến B dài: s = 24,3 km = 24300 m
Vận tốc của người đó:
\(v=\frac{s}{t}=\frac{24300}{2700}=9m/s=32,4km/h\)
Thời gian người đó đi từ A đến B là:
\(8h5'-7h20'=45'=0,75h\)
Tốc độ của người tính theo km/h là:
\(24,3\div0,75=32,4(\frac{km}{h})\)
Tốc độ của người đó tính theo m/s là:
\(32,4\div3,6=9(\frac{m}{s})\)

- Đổi : 20p = \(\dfrac{1}{3}h\) và \(2,5m/s=9km/h\), \(3m/s=10,8km/h\)
- Ta có : \(S_3=vt=\dfrac{9.1}{3}=3\left(km\right)\), \(t_2=\dfrac{S}{v}=\dfrac{3}{10,8}=\dfrac{5}{18}\left(h\right)\)
\(\Rightarrow v_{tb}=\dfrac{S}{t}=\dfrac{S_1+S_2+S_3}{t_1+t_2+t_3}=\dfrac{5+3+3}{1+\dfrac{5}{18}+\dfrac{1}{3}}=6,82\left(km/h\right)\)
Vậy ...

Vận tốc người thứ nhất đi là : `300m//p = 0,3 km//p = 18km//h`.
Vận tốc người thứ hai là: `7,5km//0,5h = 15km//h`.
Vì `18km//h > 15 km//h ->` Vận tốc người thứ nhất sẽ nhanh hơn vận tốc người thứ hai.