Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Lực hút tĩnh điện giữa electron và hạt nhân nguyên tử Hidro khi nguyên tử ở trạng thái kích thích thứ n:
Đáp án B.
+ Lực hút tính điện giữa electron và hạt nhân nguyên tử Hidro khi nguyên tử ở trạnh thái kích thích thứ n:
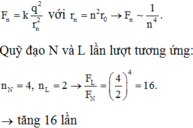
Khi electron chuyển từ L (n = 2) sang K (n = 1) phát ra phô tôn có bước sóng λ21 thỏa mãn:
\(\frac{hc}{\lambda_{21}}= E_2-E_1,(1)\)
Tương tự
\(\frac{hc}{\lambda_{32}}= E_3-E_2,(2)\)
\(\frac{hc}{\lambda_{31}}= E_3-E_1,(3)\)
Cộng (2) cho (1), so sánh với (3):
\(\frac{hc}{\lambda_{21}}+\frac{hc}{\lambda_{32}}= \frac{hc}{\lambda_{31}}\)=> \(\frac{1}{\lambda_{31}}=\frac{1}{\lambda_{21}}+\frac{1}{\lambda_{32}} \)
=> \(\lambda_{31}= \frac{\lambda_{32}\lambda_{21}}{\lambda_{32}+\lambda_{21}}.\)
. Khi nguyên tử chuyển từ trạng thái dừng có bán kính 
đến quỹ đạo dừng có bán kính 
thì lực tương tác tĩnh điện giữa êlectron và hạt nhân giảm 16 lần. Biết 
. Giá trị 
là
Năng lượng của nguyên tử ở trạng thái dừng \(n\):
\(E_n =-\frac{13,6}{n^2}.(eV)\)
Electron nhảy từ P (n=6) về K (n=1): \(hf_1 = E_6-E_1.(1)\)
Electron nhảy từ P (n=6) về L (n=2): \(hf_2 = E_6-E_2.(2)\)
Electron nhảy từ L (n=2) về K (n=1): \(hf_6 = E_2-E_1.(3)\)
Lấy (1) trừ đi (2), so sánh với (3) ta được : \(hf_1 -hf_2 = hf_3\)
=> \(f_3=f_1 -f_2.\)
+ Ta có lực tĩnh điện giữa hạt nhân và electron tỉ lệ nghịch với n4 → lực tĩnh điện giảm thì bán kính quỹ đạo tăng lên 2 lần
+ Từ khoảng giá trị của bài toán
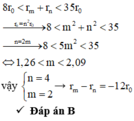
Đáp án B
+ Ta có lực tĩnh điện giữa hạt nhân và electron tỉ lệ nghịch với n 4 → lực tĩnh điện giảm thì bán kính quỹ đạo tăng lên 2 lần
+ Từ khoảng giá trị của bài toán
8 r 0 < r m + r n < 35 r 0 → r n = n 2 r 0 8 < m 2 + n 2 < 35 → n = 2 m 8 < 5 m 2 < 35 ⇔ 1 , 26 < m < 2 , 09
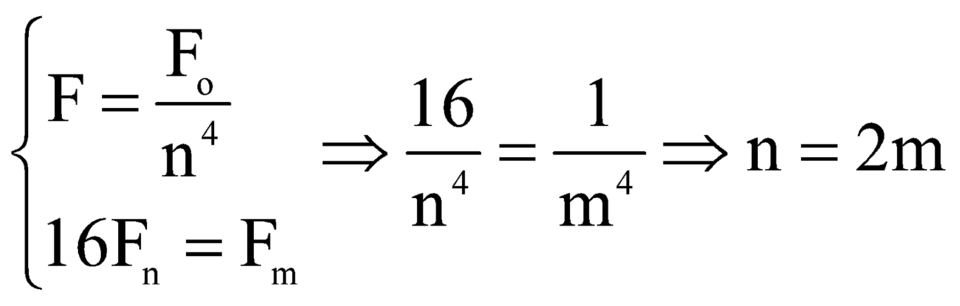
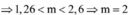
- Lực hút tính điện giữa electron và hạt nhân nguyên tử Hidro khi nguyên tử ở trạnh thái kích thích thứ n:
- Quỹ đạo N và L lần lượt tương ứng với: