Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình tổng quát: x = Acos(ωt + φ).
+ Biên độ: A = 2 đơn vị chiều dài.
+ Tần số góc: ω = 1rad/s.
+ Pha ban đầu: φ = 300 = .
Vậy đáp án đúng là : B
B. Phương trình tổng quát: x = Acos(ωt + φ).
+ Biên độ: A = 2 đơn vị chiều dài.
+ Tần số góc: ω = 1rad/s.
+ Pha ban đầu: φ = 300 = .

\(e=E_0\cos\left(\omega t+\frac{\pi}{2}\right)=E_0\sin\left(\omega t+\pi\right)\)
Pha ban đầu theo hàm sin là góc tạo bỏi véc tơ pháp tuyến mặt phẳng khung dây và véc tơ cảm ứng từ.
Suy ra: \(\alpha=\pi\)(rad)

Phương trình tổng quát: \(x= A cos(\omega t+\varphi)\)
+ Tần số góc: \(\omega = 2\pi/2 = \pi \ (rad/s)\)
+ t=0, vật qua VTCB theo chiều đương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ cm\\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình dao động: \(x = 5\cos(\pi t - \frac{\pi}{2})\) (cm)
tại sao lại ra φ=\(\dfrac{-\pi}{2}\) làm cách nào vậy bạn???

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Biên độ: \(A^2=x^2+\dfrac{v^2}{\omega^2}=(2\sqrt 3)^2+\dfrac{(20\sqrt 2)^2}{(10\sqrt 2)^2}\)
\(\Rightarrow A = 4cm\)
\(\cos\varphi = \dfrac{x}{A}=\dfrac{2\sqrt 3}{4}\)
\(v>0\Rightarrow \varphi < 0\)
Suy ra: \(\varphi=-\dfrac{\pi}{6}(rad)\)
Vậy: \(x=4\cos(10\sqrt 2 t-\dfrac{\pi}{6})(cm)\)
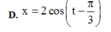

 \
\
Đáp án B
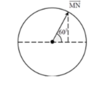
+ Vecto quay OM → biểu diễn dao động: x = 2 cos t + π 3