Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bằng cách ước lượng ta có AN' max khi d là tiếp tuyến của đường tròn và ở xa AB nhất. Dễ tìm được khi đó M ( 6;4 ) nên P = 10
Đáp án cần chọn là A

Đáp án A.
Gọi M x , y là điểm biểu diễn số phức z.
Từ giả thiết, ta có z − 4 − 3 i = 5 ⇔ x − 4 2 + y − 3 2 = 5 ⇒ M thuộc đường tròn (C) tâm I 4 ; 3 , bán kính R = 5 . Khi đó P = M A + M B , với A − 1 ; 3 , B 1 ; − 1 .
Ta có
P 2 = M A 2 + M B 2 + 2 M A . M B ≤ 2 M A 2 + M B 2 .
Gọi E 0 ; 1 là trung điểm của AB
⇒ M E 2 = M A 2 + M B 2 2 − A B 2 4 .
Do đó P 2 ≤ 4 M E 2 + A B 2 mà
M E ≤ C E = 3 5 s u y r a P 2 ≤ 4. 3 5 2 + 2 5 2 = 200.
Với C là giao điểm của đường thẳng EI
với đường tròn (C).
Vậy P ≤ 10 2 . Dấu “=” xảy ra
⇔ M A = M B M = C ⇒ M 6 ; 4 ⇒ a + b = 10.

Với ![]()
![]() Khi đó
Khi đó
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dấu bằng đạt tại
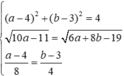
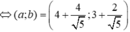
⇒ a - 2 b = - 2
Chọn đáp án B.
Mẹo trắc nghiệm: Có
![]()
![]()
![]()
Khi đó
![]()
![]()
![]()
![]()
![]()
Khi đó a-2b![]()
Chọn đáp án B.

Đáp án A.
Phương pháp:
Từ z = z ¯ + 4 - 3 i tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z = x + yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(–1;1); B(2; –3) ta có:
|z+1–i|+|z–2+3i| = MA + MB nhỏ nhất ó MA = MB
Cách giải: Gọi z = x + ui ta có:
![]()
![]()
![]()
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(–1;1); B(2; –3) ta có:
|z+1–i|+|z–2+3i| = MA + MB nhỏ nhất.
Ta có: ![]() dấu bằng xảy ra ó MA = MB => M thuộc trung trực của AB.
dấu bằng xảy ra ó MA = MB => M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có 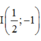 và
A
B
→
=
3
;
-
4
và
A
B
→
=
3
;
-
4
Phương trình đường trung trực của AB là 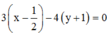
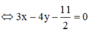
Để (MA + MB)min ó Tọa độ điểm M là nghiệm của hệ phương trình
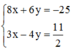
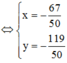
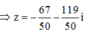

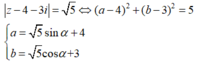
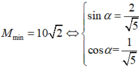
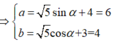

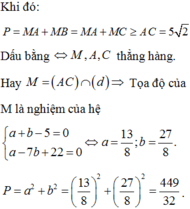
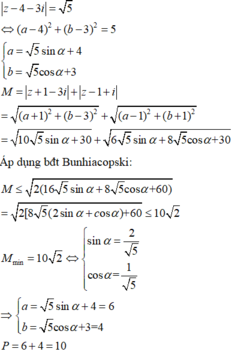
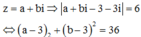

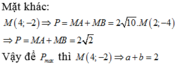
Chọn A