
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

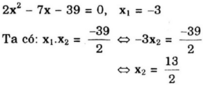

a) Vì pt có nghiệm theo vi-ét ta có :
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{8}{12}=\dfrac{2}{3}\\x_1\cdot x_2=\dfrac{1}{12}\end{matrix}\right.\)
Thay \(x_1=\dfrac{1}{2}\) ta có : \(x_2=\dfrac{2}{3}-x_1=\dfrac{2}{3}-\dfrac{1}{2}=\dfrac{1}{6}\)
b) Vì pt có nghiệm theo vi-ét ta có :
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{7}{2}\\x_1\cdot x_2=\dfrac{-39}{2}\end{matrix}\right.\)
Thay \(x_1=-3\) ta có : \(x_2=\dfrac{7}{2}-x_1=\dfrac{7}{2}-\left(-3\right)=\dfrac{13}{2}\)
c) Vì pt có nghiệm theo vi-ét ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1\cdot x_2=-2+\sqrt{2}\end{matrix}\right.\)
Thay \(x_1=-\sqrt{2}\) ta có : \(x_2=-1-x_1=-1-\left(-\sqrt{2}\right)=\sqrt{2}-1\)
d) Thay \(x_1=2\) vào pt ta có
\(2^2-2m\cdot2+m-1=0\)
\(\Leftrightarrow4-4m+m-1=0\\ \Leftrightarrow3-3m=0\\ \Leftrightarrow-3m=-3\\ \Leftrightarrow m=1\)
Vì pt \(x^2-2mx+m-1=0\) có nghiệm theo vi-ét ta có
\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1\cdot x_2=m-1\end{matrix}\right.\)
Thay \(x_1=2\) ta có :
\(x_2=2m-x_1=2\cdot1-2=0\)

Theo định lý Vi-et ta có: phương trình
a
x
2
+
b
x
+
c
= 0 có hai nghiệm
x
1
;
x
2
thì: 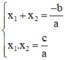
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 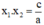
(Các bạn có thể làm cách 2 sử dụng điều kiện 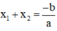 ).
).
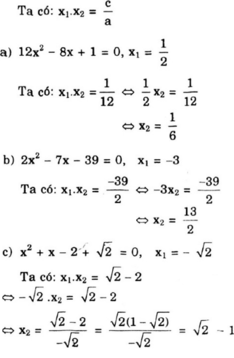
d) x 2 - 2 m x + m - 1 = 0 ( 1 )
Vì x 1 = 2 là một nghiệm của pt (1) nên:
2 2 - 2 m . 2 + m - 1 = 0
⇔ 4- 4 m+ m – 1 = 0
⇔ 3- 3m = 0
⇔ m = 1
Khi m = 1 ta có: x 1 . x 2 = m - 1 (hệ thức Vi-ét)
⇔ 2 . x 2 = 0 ( v ì x 1 = 2 và m = 1)
⇔ x 2 = 0

x2 - 2mx + m - 1 = 0 (1)
Vì x1 = 2 là một nghiệm của pt (1) nên:
22 - 2m.2 + m - 1 = 0
⇔ 4- 4 m+ m – 1 = 0
⇔ 3- 3m = 0
⇔ m = 1
Khi m = 1 ta có: x1.x2 = m - 1 (hệ thức Vi-ét)
⇔ 2.x2 = 0 (vì x1 = 2 và m = 1)
⇔ x2 = 0

Theo định lý Vi-et ta có: phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2 thì: 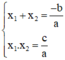
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 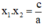
(Các bạn có thể làm cách 2 sử dụng điều kiện 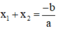 ).
).
Ta có: x 1 . x 2 = c a

a) Dùng hệ thức Viét ta có:
\(x_1x_2=\dfrac{-35}{1}=-35\\ \Leftrightarrow7x_2=-35\\ \Leftrightarrow x_2=-5\\ x_1+x_2=\dfrac{-m}{1}=-m\\ \Leftrightarrow7+\left(-5\right)=-m\\ \Leftrightarrow-m=2\\ \Leftrightarrow m=-2\)
b) Dùng hệ thức Viét ta có:
\(x_1+x_2=\dfrac{-\left(-13\right)}{1}=13\\ \Leftrightarrow12,5+x_2=13\\ \Leftrightarrow x_2=0,5\\ x_1x_2=\dfrac{m}{1}=m\\ \Leftrightarrow12,5\cdot0,5=m\\ \Leftrightarrow m=6,25\)
c) Dùng hệ thức Viét ta có:
\(x_1+x_2=\dfrac{-3}{4}\\ \Leftrightarrow-2+x_2=\dfrac{-3}{4}\\ \Leftrightarrow x_2=\dfrac{5}{4}\\ x_1x_2=\dfrac{-m^2+3m}{4}\\ \Leftrightarrow4x_1x_2=-m^2+3m\\ \Leftrightarrow4\cdot\left(-2\right)\cdot\dfrac{5}{4}+m^2-3m=0\\ \Leftrightarrow m^2-3m-10=0\\ \Leftrightarrow m^2-5m+2m-10=0\\ \Leftrightarrow m\left(m-5\right)+2\left(m-5\right)=0\\ \Leftrightarrow\left(m+2\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2\\m=5\end{matrix}\right.\)
d) Dùng hệ thức Viét ta có:
\(x_1x_2=\dfrac{5}{3}\\ \Leftrightarrow\dfrac{1}{3}x_2=\dfrac{5}{3}\\ \Leftrightarrow x_2=5\\ x_1+x_2=\dfrac{-\left[-2\left(m-3\right)\right]}{3}=\dfrac{2\left(m-3\right)}{3}=\dfrac{2m-6}{3}\\ \Leftrightarrow3\left(x_1+x_2\right)=2m-6\\ \Leftrightarrow3\left(\dfrac{1}{3}+5\right)=2m-6\\ \Leftrightarrow3\cdot\dfrac{16}{3}+6=2m\\ \Leftrightarrow16+6=2m\\ \Leftrightarrow22=2m\\ \Leftrightarrow m=11\)

a: Thay x=-3 vào pt,ta được:
\(3\cdot\left(-3\right)^2+2\cdot\left(-3\right)-21=0\left(đúng\right)\)
\(x_1+x_2=-\dfrac{2}{3}\)
=>x2=-2/3+3=7/3
b: Thay x=5 vào pt, ta được:
\(-4\cdot5^2-3\cdot5+115=0\left(đúng\right)\)
\(x_1+x_2=\dfrac{3}{-4}=-\dfrac{3}{4}\)
nên x2=-3/4-5=-23/4