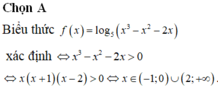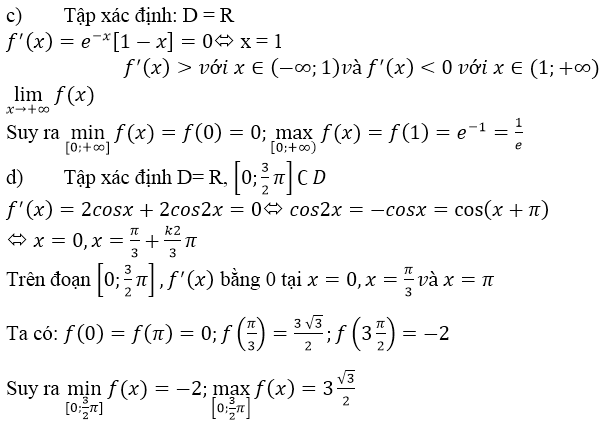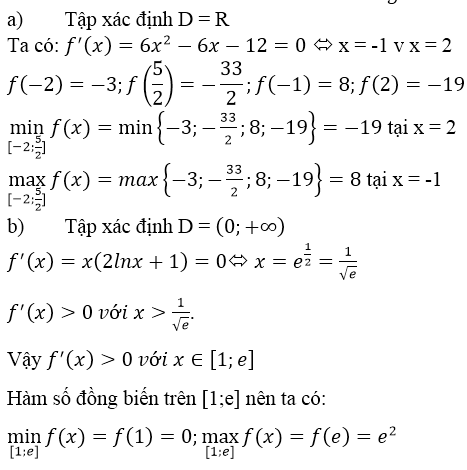Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) f(x) = 2x3 – 3x2 – 12x + 1 ⇒ f’(x) = 6x2 – 6x – 12
f’(x) = 0 ⇔ x ∈ {-1, 2}
So sánh các giá trị:
f(x) = -3; f(-1) = 8;
f(2) = -19, f(52)=−332f(52)=−332
Suy ra:
maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19
b) f(x) = x2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e] nên f(x) đồng biến.
Do đó:
maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0
c) f(x) = f(x) = xe-x ⇒ f’(x)= e-x – xe-x = (1 – x)e-x nên:
f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1) và f’(x) < 0, ∀x ∈ (1, +∞)
nên:
maxx∈[0,+∞)f(x)=f(1)=1emaxx∈[0,+∞)f(x)=f(1)=1e
Ngoài ra f(x) = xe-x > 0, ∀ x ∈ (0, +∞) và f(0) = 0 suy ra
maxx∈[0,+∞)f(x)=f(0)=0maxx∈[0,+∞)f(x)=f(0)=0
d) f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x
f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π
⇔ x∈{−π+k2π;π3+k2π3}x∈{−π+k2π;π3+k2π3}
Trong khoảng [0,3π2][0,3π2] , phương trình f’(x) = 0 chỉ có hai nghiệm là x1=π3;x2=πx1=π3;x2=π
So sánh bốn giá trị : f(0) = 0; f(π3)=3√32;f(π)=0;f(3π2)=−2f(π3)=332;f(π)=0;f(3π2)=−2
Suy ra:
maxx∈[0,3π2]f(x)=f(π3)=3√32minx∈[0,3π2]f(x)=f(3π2)=−2

Bài 3:
Áp dụng các hằng đẳng thức đáng nhớ ta có:
$C=a^4+b^4=(a^2+b^2)^2-2a^2b^2$
$=[(a+b)^2-2ab]^2-2(ab)^2$
$=(8^2-2.15)^2-2.15^2=706$
Bài 2:
a)
$D=-x^2+6x-11=-11-(x^2-6x)=-2-(x^2-6x+9)$
$=-2-(x-3)^2$
Vì $(x-3)^2\geq 0$ với mọi $x$ nên $D=-2-(x-3)^2\leq -2$
Vậy GTLN của $D$ là $-2$ khi $(x-3)^2=0\Leftrightarrow x=3$
b)
$F=4x-x^2+1=1-(x^2-4x)=5-(x^2-4x+4)=5-(x-2)^2$
$\leq 5-0=5$
Vậy $F_{\max}=5$. Giá trị này được khi $(x-2)^2=0\leftrightarrow x=2$