Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Gọi vectơ pháp tuyến của mặt phẳng (P) là ![]() , a²+b²+c²>0.
, a²+b²+c²>0.
Phương trình mặt phẳng (P): a(x-4)+b (y-3)+c (z-4)=0.
Do (P) // Δ nên -3a+2b+2c=0 => 3a = 2 (b + c)
Mặt phẳng (P) tiếp xúc với (S) nên
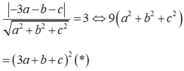
Thay 3a=2 (c+b ) vào (*) ta được:
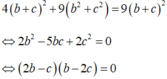
TH1: 2b-c=0, chọn b=1; c=2 => a = 2 => (P): 2x+y+2z-19=0 (thỏa).
TH2: b-2c=0, chọn c=1; b=2 => a = 2 => (P): 2x+2y+z-18=0 (loại do Δ ⊂ (P))

Đáp án B
Pt pháp tuyến của mặt phẳng cần tìm là n ⇀ = d , ⇀ ∆ ⇀ = (1;0;1)
Pt có dạng: x+z+D=0
Khoảng cách từ O (-1;1;-2) đến mp là 2
⇒ D=1
Pt có dạng : x+z+1=0

Gọi mặt phẳng là (P) dễ kí hiệu
\(d\left(M;\left(P\right)\right)=\frac{\left|-6+2+2-7\right|}{\sqrt{2^2+2^2+1}}=\frac{9}{3}=3\)
Áp dụng định lý Pitago:
\(R=\sqrt{3^2+4^2}=5\)
Phương trình mặt cầu:
\(\left(x+3\right)^2+\left(y-1\right)^2+\left(z-2\right)^2=25\)
\(\Leftrightarrow x^2+y^2+z^2+6x-2y-4z-11=0\)

\(\left\{{}\begin{matrix}\overrightarrow{n_{\left(P1\right)}}=\left(1;-1;1\right)\\\overrightarrow{n_{\left(P2\right)}}=\left(3;2;-12\right)\end{matrix}\right.\) \(\Rightarrow\)\(\left[\overrightarrow{n_{\left(P1\right)}};\overrightarrow{n_{\left(P2\right)}}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Chọn \(\overrightarrow{n_{\left(p\right)}}=\left(2;3;1\right)\) là 1 vtpt của (P)
Phương trình (P): \(2x+3y+z=0\)
Câu 2:
\(\left\{{}\begin{matrix}\overrightarrow{u_d}=\left(2;1;1\right)\\\overrightarrow{u_{d'}}=\left(1;-2;1\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{u_d};\overrightarrow{u_{d'}}\right]=\left(3;-1;-5\right)\)
\(\Rightarrow\) Chọn \(\overrightarrow{n_{\alpha}}=\left(3;-1;-5\right)\) là một vtpt của \(\left(\alpha\right)\)
Phương trình \(\left(\alpha\right)\):
\(3\left(x-0\right)-1\left(y-1\right)-5\left(z-2\right)=0\)
\(\Leftrightarrow3x-y-5z+11=0\)

Gọi vecto chỉ phương của tiếp tuyến là \(\overrightarrow{u}_{(a,b,c)}\). Ta có :
\(\overrightarrow {AC}=(-1,-1,0);\overrightarrow {n}_{P}=(2,1,1)\)
Theo điều kiện đề bài \(\overrightarrow{u}\perp \overrightarrow{AC},\overrightarrow{u}\perp \overrightarrow{n}_{P}\Rightarrow \overrightarrow{u}=[\overrightarrow{AC},\overrightarrow{n}_{P}]=(-1,1,1)\)
Do đó phương tiếp tuyến có dạng \(\frac{x-2}{-1}=y-2=z\), tức đáp án $B$ là đáp án đúng




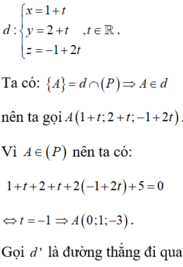
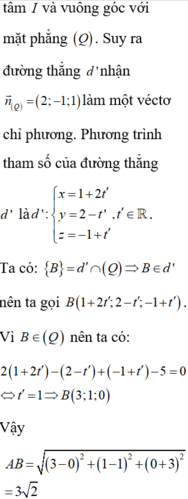
Chọn B.
Mặt cầu (S) tâm I(-1;2;3) và
Do mặt phẳng (α)//(P) nên (α) có dạng : x + 2y - 2z + m = 0.
Do (α) tiếp xúc với (S) ⇔ d(I,(α)) = R.
* Với m = - 6 suy ra mặt phẳng có phương trình: x + 2y - 2z - 6 = 0.
* Với m = 12 suy ra mặt phẳng có phương trình: x + 2y - 2z + 12 = 0.