
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



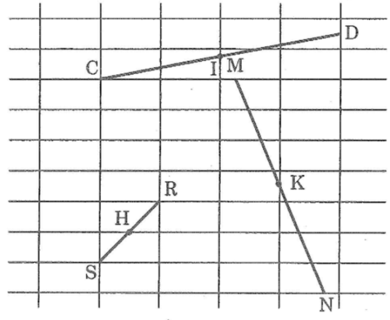
Hãy xem 2 điểm C và D nằm trên 2 đường thẳng song song nào của hình 19, trung điểm của đoạn thẳng CD là giao điểm của CD và 1 trog các đường của hình 19 sog sog vs 2 đường thẳng đó . Cx vẽ như vậy đối vs trung điểm của các đoạn thẳng MN , RS



Gọi số học sinh khối 7 của trường đó là : b (học sinh)
Gọi số học sinh khối 8 của trường đó là : c (học sinh)
Gọi số học sinh khối 9 của trường đó là : d (học sinh)
Với điều kiện :a>0;b>0;c>;d>0 (*).
Theo đề bài, tổng số học sinh khối 6 và khối 7 chiếm \(\dfrac{25}{44}\) tổng số học sinh toàn trường,nên :
a+b= \(\dfrac{25}{44}\)\(\times\)1320=750 (1)
Số học sinh khối 8 chiếm 25% số học sinh toàn trường nên:
c=25% \(\times\)1320=330 (học sinh)
Số học sinh khối 8 là : d=1320 \(-\)(a+b)\(-\)c
= 1320 \(-\)750 \(-\)330 = 240 (học sinh)
Theo bài ra, tổng số học sinh khối 6 và khối 8 bằng 2 lần số học sinh khối 7 ,nên:
a+c=2b (2)
Từ (1)và (2) ,ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=750\\a+c=2b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-b\\750-b+330=2b\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a=750-b\\1080-b=2b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-b\\-b-2b=-1080\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a=750-b\\-3b=-1080\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=750-360=390\\b=360\end{matrix}\right.\)thỏa mản(*)
Vậy khối 6 có 390 (học sinh), khối 7có 360(học sinh), khối 8 có 330 (học sinh), khối 9 có 240 (học sinh).

Hãy xem 2 điểm C và D nằm trên hai đường thẳng song song nào của hình 19 , trung điểm của đoạn thẳng CD là giao điểm của CD và 1 trong các đường của hình 19 song song với 2 đường thẳng đó . Cũng vẽ như vậy đối với trung điểm của các đoạn thẳng MN,RS .

Bài 1 :
a) A=37.36+20.37+44.37
A=37.(36+20+44)
A=37.100
A=3700
Bài 6 :
\(A=2^0+2^1+2^2+2^3+...+2^{2010}\)
\(2A=2+2^2+2^3+2^4+...+2^{2011}\)
\(2A-A=\left(2+2^2+2^3+2^4+...+2^{2011}\right)-\left(2^0+2^1+2^2+2^3+...+2^{2010}\right)\)
\(A=\left(2+2^2+2^3+2^4+...+2^{2010}\right)+2^{2011}-2^0-\left(2+2^2+2^3+2^4+...+2^{2010}\right)\)
\(A=2^{2011}-1\)
\(\Rightarrow A+1=2^{2011}\)
Vậy A đã có dạng lũy thừa cơ số là 2

\(2M=\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{12-10}{10.11.12}=\)
\(=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{10.11}-\frac{1}{11.12}=\frac{1}{2}-\frac{1}{11.12}\)
\(\Rightarrow M=\frac{1}{4}-\frac{1}{11.24}=\frac{66-1}{11.24}=\frac{65}{11.24}\)