K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

L
31 tháng 3 2016
F O
a. Ta có: \(d'=20,\frac{h'}{h}=\left|\frac{d'}{d}\right|\Rightarrow d=10cm\)
\(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\Rightarrow f=\frac{20}{3}cm\)
\(k=-\frac{d'}{d}=-2\)
b. Vật cách ảnh \(90cm\Rightarrow d_1+d'_1=-90cm\) và \(d'_1<0\) (ảnh ảo)
\(\frac{1}{d_1}+\frac{1}{d'_1}=\frac{3}{20}\)
Giải 2 pt tìm được vị trí vật mới.

SS
31 tháng 3 2016
\(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)
Thấu kính phân kì nên \(f<0\)
Vật AB là vật thật nên \(d>0\)
Thấu kính phân kì cho ảnh ảo nên \(d'<0\)
Theo đề bài ta có:
\(\frac{1}{-30}=\frac{1}{d}+\frac{1}{d'}\)
\(\left|d\right|+\left|d'\right|=25\Rightarrow d-d'=25\)
Giải hệ ta được: \(d=15cm,d'=-10cm\)
Hay vật cách thấu kính 15cm, ảnh cách thấu kính 10cm




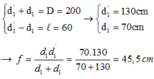


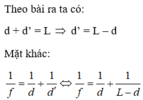





Đáp án A
Đây là bài toán trong đó khoảng cách giữa vật và ảnh thật không đổi bằng D và cùng một thấu kính đặt ở hai vị trí khác nhau. Điều này hoàn toàn khác với bài toán hệ hai thấu kính
Áp dụng nguyên lý thuận nghịch chiều truyền ánh sáng:
Từ công thức 1 f = 1 d + 1 d ' ta thấy: công thức có tính đối xứng đối với d và d'
Vì nếu hoán vị d và d' thì công thức không thay đổi gì cả. Nói cách khác nếu vật cách thấu kính d cho ảnh thấu kính d' thì ngược lại, nếu vật cách thấu kính d' sẽ cho ảnh cách thấu kính là D
Nếu gọi d 1 , d ' 1 tương ứng là khoảng cách vật và ảnh tới thấu kính ở vị trí (1) và d 2 , d ' 2 là khoảng cách vật và ảnh tới thấu kính ở vị trí (2) thì ta có mối liên hệ: d 1 = d ' 2 và d ' 1 = d 2
Vậy ta có: d 1 + d ' 1 = D và d 2 − d 1 = d ' 1 − d 1 = 1
⇒ d 1 = D + 1 2 và d ' 1 = D − 1 2 ⇒ 1 f = 1 d 1 + 1 d ' 1 = 4 D D 2 − l 2 ⇒ f = D 2 − l 2 4 D ( 1 )
Biện luận: Từ (1) ta rút ra được 4 D f = D 2 − I 2
⇒ D 2 − 4 D f = l 2 > 0 ⇒ D D − 4 f ⇒ D > 4 f
Vậy muốn có được hai vị trí của thấu kính cho ảnh rõ nét trên màn thì điều kiện là khoảng cách vật – màn phải lớn hớn 4f
Đặc biệt nếu l = 0 tức là D = 4 f thì chỉ có một vị trí của thấu kính cho ảnh rõ nét trên màn E
Áp dụng: D = 200 c m và l = 120 c m ⇒ f = 32 c m