Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
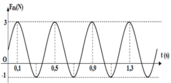
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
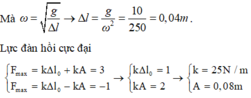
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại → φ 0 = π 2 rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm.

Đáp án D
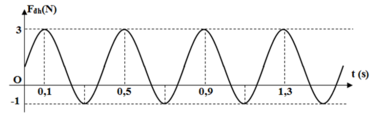
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Mà
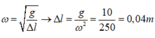
Lực đàn hồi cực đại
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại
→  rad.
rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm

Đáp án D
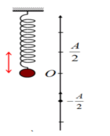
Độ giãn của con lắc ở vị trí cân bằng: T = 0,4 s = 2 π ∆ l 0 g ⇒ ∆ l 0 = T 2 g 4 π 2 = 0 , 04 m = 4 cm
Lực đàn hồi của con lắc tại hai vị trí biên:
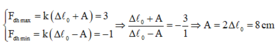
Độ cứng của lò xo: k = F d h m a x ∆ l 0 + A = 3 0 , 04 + 0 , 08 = 25 N / m
Biểu thức lực đàn hồi:
![]()
Tại thời điểm t = 0,1 s , lực đàn hồi có giá trị F = 3N nên:
F d h = 1 + 2 cos ( 5 π . 0 , 1 + μ ) = 3
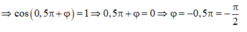
Phương trình dao động của vật: x = 8 cos ( 5 πt - π 2 ) ( c m )

Đáp án B
Phương pháp: Sử dụng lí thuyết về lực đàn hồi của con lắc lò xo đặt thẳng đứng
Cách giải:
Ở VTCB lò xo dãn một đoạn ∆ l . Ta có
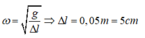
Biên độ dao động A = 5cm
Khi ở vị trí cao nhất, lò xo không biến dạng nên lực đàn hồi của lò xo có độ lớn bằng 0.

+ Tại vị trí lực đàn hồi của lò xo bằng 12 N ta có:
F d h = m g + k x → k x = 12 − 1.10 = 2 = F k v với x chính là biên độ dao động của vật.
+ Mặc khác: k . Δ l = m g = 10 > k A
® Δ l > A
® Lực đàn hồi nhỏ nhất tác dụng lên vật là: F d h min = k Δ l − A = k Δ l − k A = 10 − 2 = 8 N
Đáp án C

Gọi biên độ dao động là A.
Độ dãn của lò xo khi vật ở VTCB là: \(\Delta\ell_0=\dfrac{mg}{k}\)
Độ dãn cực đại của lò xo là: \(\Delta\ell_0+A=10cm=0,1m\)
Lực đàn hồi cực tiểu là: \(k(\Delta\ell_0-A)=0,8\)
\(\Rightarrow k(\Delta \ell_0+\Delta\ell_0-0,1)=0,8\)
\(\Rightarrow k(2\Delta \ell_0-0,1)=0,8\)
\(\Rightarrow k(2\dfrac{mg}{k}-0,1)=0,8\)
\(\Rightarrow2.mg-0,1.k=0,8\)
\(\Rightarrow2.0,24.10-0,1.k=0,8\)
\(\Rightarrow k=40(N/m)\)
Lực mà lò xo tác dụng lên vật khi lò xo dãn 5cm là lực đàn hồi của lò xo và bằng: \(F=k.\Delta\ell=40.0,05=2(N)\)



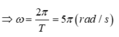
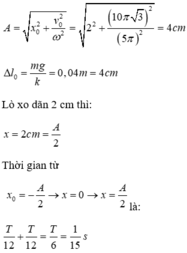
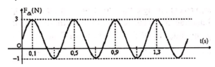
Chọn C