Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc toạ độ O ở đỉnh tháp, trục toạ độ ox theo hướng v0 trục oy thẳng đứng xuống dưới.
Gốc thời gian là lúc ném vật.
Theo phương ox: Vật chuyển động thẳng đều với vận tốc vx = v0; x0 = 0
Theo phương oy: vật chuyển động nhanh dần đều với vận tốc đầu v0y = 0 ; y0 = 0
a. Phương trình toạ độ của quả cầu:
=> x = v0t => x = 20t (a)
=> y = 1/2 gt2 => y = 5t2 (b)
Lúc t = 2s => x = 40m => y = 60m
b. Phương trình quỹ đạo của quả cầu:
Từ (a) => t = x/20 thế vào (b) ta có :
\(y=5\left(\frac{x}{20}\right)^2=\frac{1}{80}x^2\left(m\right)\) (\(x\ge0\))
=> Quỹ đạo là đường Parabol, đỉnh O
c.Khi quả cầu chạm đất thì y = 80 m
Ta có y = 1/80 x2 = 80 => x = 80 m
Quả cầu chạm đất tại nơi cách chân tháp 80 m
Vận tốc quả cầu: \(v=\sqrt{v^2_x+v_y^2}=\sqrt{v_0^2+\left(gt\right)^2}\)
Thời gian để quả cầu chạm đất
\(t=\frac{2y}{9}=4s\)
Vậy : v = \(\sqrt{20^2+\left(10.4\right)^2}\approx44,7\) m/s

Chọn đáp án A
+ Chọn gốc tọa độ O tại nơi ném vật, trục tọa độ OXY như hình vẽ, gốc thời gian là lúc vừa ném vật. Phương trình quỹ đạo của quả cầu
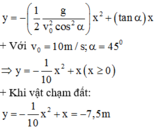
+ Giải phương trình và loại nghiệm âm ta suy ra x = 15m
+ Quả cầu chạm đất tại nơi cách vị trí ban đầu theo phương ngang là 15m
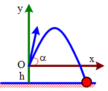

Đáp án A
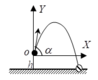
Chọn gốc tọa độ O tại nơi ném vật, trục tọa độ OXY như hình vẽ, gốc thời gian lúc vừa ném vật. Phương trình quỹ đạo của quả cầu:
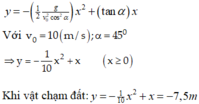
Giải phương trình và loại nghiệm âm, ta suy ra x=15m.
Quả cầu chạm đất tại nơi cách vị trí ban đầu theo phương ngang là 15m

a) Phương trình tọa độ : \(\left\{{}\begin{matrix}x=v_0t=20t\\y=\dfrac{1}{2}gt^2=5t^2\end{matrix}\right.\)
b) Phương trình quỹ đạo : \(x=20t\rightarrow t=\dfrac{x}{20}\rightarrow y=\dfrac{1}{2\cdot20^2}\cdot10\cdot x^2=\dfrac{x^2}{80}\)
c) Tầm xa \(L=v_0\sqrt{\dfrac{2h}{g}}=20\sqrt{\dfrac{2\cdot80}{10}}=80\left(m\right)\)
Vận tốc khi chạm đất: \(v=\sqrt{v_0^2+2hg}=\sqrt{20^2+2\cdot80\cdot10}=44,7\left(m/s\right)\)

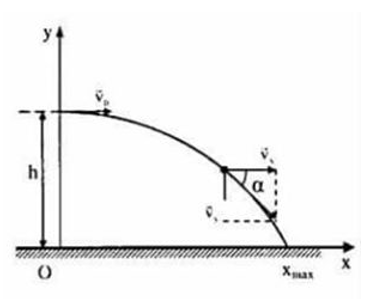
Chọn gốc tọa độ tại mặt đất.
\(v_0\) là vận tốc ban đầu vật.
\(Ox:\left\{{}\begin{matrix}v_x=v_0=hằngsố\\x=v_0\cdot t\end{matrix}\right.\)
\(Oy:\left\{{}\begin{matrix}v_y=g\cdot t\\y=h-\dfrac{1}{2}gt^2\end{matrix}\right.\)
Tại thời điểm \(t=4a;\alpha=30^o\)\(\Rightarrow v_x=v_y\)
\(\Rightarrow v_0=g\cdot t=10\cdot4=40\)m/s
Thời gian vật chạm đất\(\left(y=0\right)\)
\(\Rightarrow h-\dfrac{1}{2}gt^2=0\Rightarrow h=\dfrac{1}{2}gt^2\)
\(\Rightarrow t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot180}{10}}=6s\)
Phương trình quỹ đạo của quả cầu:
\(y=\dfrac{g}{2v_0^2}\cdot x^2=\dfrac{10}{2\cdot40^2}\cdot x^2=\dfrac{x^2}{320}\)
Vận tốc khi chạm đất:
\(v=\sqrt{v^2_0+\left(g\cdot t\right)^2}=\sqrt{40^2+\left(10\cdot4\right)^2}=40\sqrt{2}\)m/s
Khi đó góc tính đc:
\(v^2=v^2_0+\left(g\cdot t\right)^2=\left(v_0\cdot cos\beta\right)^2\)
\(\Rightarrow v=v_0\cdot cos\beta\Rightarrow cos\beta=\dfrac{v}{v_0}=\dfrac{40\sqrt{2}}{40}=\sqrt{2}\)
Hơi vô lí



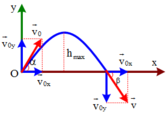

Chọn hệ quy chiếu Oxy như hình vẽ
Thời điểm ban đầu
Chiếu lên trục ox có
x 0 = 0 ; v 0 x = v 0 cos α = 20. 1 2 = 10 m / s
Chiếu lên trục oy có: y 0 = 0
v 0 y = v 0 sin α = 20. 3 2 = 10 3 m / s
Xét tại thời điểm t có a x = 0 ; a y = − g
Chiếu lên trục ox có
v x = 10 ; x = 10 t
Chiếu lên trục oy có: v y = 10 3 − 10 t ; y = 10 3 t − 5 t 2
⇒ y = 3 x − x 2 20 Vậy quỹ đạo của vật là một parabol
b. khi vật 2s ta có x = 10.2 = 20 m ; y = 10 3 .2 − 5.2 2 = 14 , 641 m
Vận tốc của vật lức 2s là v 1 = v 1 x 2 + v 1 y 2
với v 1 x = 10 m / s ; v 1 y = 10 3 − 10.2 = − 2 , 68 m / s
⇒ v 1 = 10 2 + − 2 , 68 2 = 10 , 353 m / s
c. Khi chạm đất y = 0 ⇒ 3 x − x 2 20 = 0 ⇒ x = 20 3 m
và 10 3 t − 5 t 2 = 0 ⇒ t = 2 3 s
Vật chạm đất cách vị trí ném là 20 3 m
Vận tốc khi chạm đất v = v x 2 + v y 2
với v x = 10 m / s ; v y = 10 3 − 10.2 3 = − 10 3 m / s
⇒ v = 10 2 + − 10 3 2 = 20 m / s